练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知四棱锥的底面为直角梯形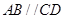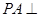，，，底面，且，是的中点.
    ⑴求证：直线平面；
    ⑵若直线与平面所成的角为，求四棱锥的体积.

    ⑴见解析;⑵1

    解析试题分析：⑴要证直线平面,需要在平面内找到一条与平行的直线.显然不容易找到;故考虑利用面面平行退出线面平行, 取的中点,构造平面,根据 ,∥可证.
    ⑵利用体积公式.需求出梯形的面积,根据底面,可知.
    试题解析：⑴证明：取的中点，则，故平面;
    又四边形正方形，∴∥，故∥平面;
    ∴平面平面,
    ∴平面.
    ⑵根据⑴可知,平面.所以根据题意有;
    因为四边形为正方形,所以为等腰直角三角形.所以,
    根据可知，又因为底面,所以棱锥的高为.
    因为梯形的面积为,故.

    考点：利用面面平行证明线面平行;棱锥体积;

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    如图，四边形ABCD是梯形，四边形CDEF是矩形，且平面ABCD⊥平面CDEF，∠BAD＝∠CDA＝90°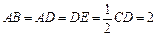，，M是线段AE上的动点．
    （1）试确定点M的位置，使AC∥平面MDF，并说明理由；
    （2）在（1）的条件下，求平面MDF将几何体ADE－BCF分成的两部分的体积之比．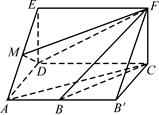

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

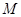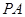    已知圆锥母线长为6，底面圆半径长为4，点是母线的中点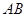，是底面圆的直径，半径与母线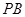所成的角的大小等于．

    （1）求圆锥的侧面积和体积．
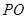    （2）求异面直线与所成的角；

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知圆台的上、下底面半径分别是2、6，且侧面面积等于两底面面积之和。
    （1）求该圆台的母线长；（2）求该圆台的体积。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图,直三棱柱ABCA′B′C′,∠BAC=90°,AB=AC=,AA′=1,点M,N分别为
    A′B和B′C′的中点.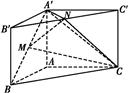

    (1)证明:MN∥平面A′ACC′;
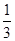    (2)求三棱锥A′MNC的体积.(锥体体积公式V=Sh,其中S为底面面积,h为高)

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图①所示，在Rt△ABC中，AC＝6，BC＝3，∠ABC＝90°，CD为∠ACB的平分线，点E在线段AC上，CE＝4.如图②所示，将△BCD沿CD折起，使得平面BCD⊥平面ACD，连结AB，设点F是AB的中点．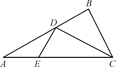
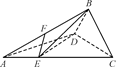    图①图②
    (1)求证：DE⊥平面BCD；
    (2)若EF∥平面BDG，其中G为直线AC与平面BDG的交点，求三棱锥B-DEG的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图所示,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF⊥平面EFDC,设AD中点为P.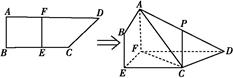

    (1)当E为BC中点时,求证:CP∥平面ABEF;
    (2)设BE=x,问当x为何值时,三棱锥ACDF的体积有最大值?并求出这个最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图，四面体ABCD中，△ABC与△DBC都是边长为4的正三角形．

    (1)求证：BC⊥AD；
    (2)试问该四面体的体积是否存在最大值？若存在，求出这个最大值及此时棱长AD的大小；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在等腰梯形ABCD中，AB∥CD，AB＝BC＝AD＝2，CD＝4，E为边DC的中点，如图1.将△ADE沿AE折起到△AEP位置，连PB、PC，点Q是棱AE的中点，点M在棱PC上，如图2.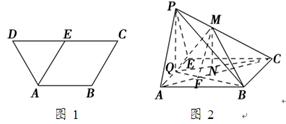

    (1)若PA∥平面MQB，求PM∶MC；
    (2)若平面AEP⊥平面ABCE，点M是PC的中点，求三棱锥A­MQB的体积．

    查看答案和解析>>

    同步练习册答案