
(本小题满分12分)已知f (x)=(1+x)m+(1+2x)n(m,n∈N*)的展开式中x的系数为11.
(1)求x2的系数的最小值;
(2)当x2的系数取得最小值时,求f (x)展开式中x的奇次幂项的系数之和.
解: (1)由已知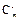 +2
+2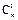 =11,∴m+2n=11,x2的系数为
=11,∴m+2n=11,x2的系数为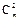 +22
+22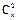 =
=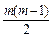 +2n(n-1)=
+2n(n-1)=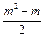 +(11-m)(
+(11-m)(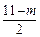 -1)=(m-
-1)=(m-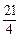 )2+
)2+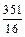 .
.
∵m∈N*,∴m=5时,x2的系数取最小值22,此时n=3.
(2)由(1)知,当x2的系数取得最小值时,m=5,n=3,
∴f (x)=(1+x)5+(1+2x)3.设这时f (x)的展开式为f (x)=a0+a1x+a2x2+…+a5x5,
令x=1,a0+a1+a2+a3+a4+a5=25+ 33,
33,
令x=-1,a0-a1+a2-a3+a4-a5=-1,
两式相减得2(a1+a3+a5)=60, 故展开式中x的奇次幂项的系数之和为30.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:解答题
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少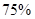 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
(Ⅰ)求所选的两个小区恰有一个为“非低碳小区”的概率;
(Ⅱ)假定选择的“非低碳小区”为小区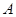 ,调查显示其“低碳族”的比例为
,调查显示其“低碳族”的比例为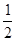 ,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区
,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区 是否达到“低碳小区”的标准?
是否达到“低碳小区”的标准?
|
|

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有6本不同的书,按照以下要求处理,各有多少种不同的分法?
(1)一堆一本,一堆两本,一堆三本;
(2)甲得一本,乙得两本,丙得三本;
(3)一人得一本,一人得二本,一人得三本;
(4)平均分给甲、乙、丙三人;
(5)平均分成三堆.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有4名男生、5名女生,全体排成一行,问下列情形各有多少种不同的排法?
(1)甲不在中间也不在两端;
(2)甲、乙两人必须排在两端;
(3)男、女生分别排在一起;
(4)男女相间;
(5)甲、乙、丙三人从左到右顺序保持一定.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)号码为1、2、3、4、5、6的六个大小相同的球,放入编号为1、2、3、4、5、6的六个盒子中,每个盒子只能放一个球.
(Ⅰ)若1号球只能放在1号盒子中,2号球只能放在2号的盒子中,则不同的放法有多少种?
(Ⅱ)若3号球只能放在1号或2号盒子中,4号球不能放在4号盒子中,则不同的放法有多少种?
(Ⅲ)若5、6号球只能放入号码是相邻数字的两个盒子中,则不同的放法有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com