Question

甲、乙两地相距s千米，汽车从甲地匀速驶到乙地，速度不得超过c千米/时，已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度v(千米/时)的平方成正比，比例系数为b；固定部分为a元.

（1）把全程运输成本y（元）表示为速度v(千米/时)的函数，并指出这个函数的定义域；

（2）为了使全程运输成本最小，汽车应以多大速度行驶？

Answer 1

思路解析：本题写出函数y=f(v)=(+bv)s及其定义域（0,c）并不难，在运用不等式的平均值定理求y的最小值时，确定其中等号成立条件时,要由=bv解出v=后检验是否在函数定义域（0,c］内.这时要对与c的大小作出讨论,并且对于＞c的情形，求y的最小值还要另选方法，即选择通过研究函数单调性而确定其最值的方法.这是一种运用概念的一般方法，不过运用时过程比较烦琐就是了.

解：（1）依题意得汽车从甲地匀速行驶到乙地所用时间为（时），全程运输成本为y=a·+bv²·=s(+bv).

∴函数为y=s(+bv)，其定义域为（0,c）.

（2）依题意得s、a、b、v均为正数，则s(+bv)≥2s=2s.当且仅当=bv，即v=时，上式“≥”处等号成立.

若≤c，则当v=时，y取最小值.

若＞c时，任取v₁、v₂，使0＜v₁＜v₂≤c＜,

则(+bv₂)-(+bv₁)=b(v₂-v₁)+a()=(bv₁v₂-a).

由于v₁v₂＞0,v₂-v₁＞0，并且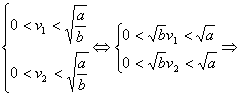bv₁v₂＜a，

∴+bv₂＜+bv₁.

又s＞0,故s(+bv₂)＜s(+bv₁).

∴当＞c时，v的函数y=s(+bv)在区间（0,c］上是减函数，当v=c时，y取最小值.

综上，可知为了使全程运输成本最小，当≤c时，汽车行驶速度应为v=（千米/时）；当＞c时，汽车行驶速度应为v=c（千米/时）.