
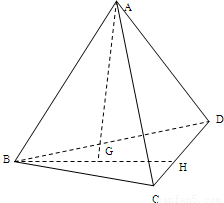
 如图所示,设A为△ABC所在平面外一点,HD=2CH,G为BH的中点
如图所示,设A为△ABC所在平面外一点,HD=2CH,G为BH的中点| AB |
| AC |
| AD |
| AG |
| AB |
| AC |
| AD |
| AG |
| AG |
| 1 |
| 2 |
| AB |
| AH |
| 1 |
| 2 |
| AB |
| 1 |
| 3 |
| AC |
| 1 |
| 6 |
| AC |
| AG |
| 1 |
| 2 |
| AB |
| AH |
| 1 |
| 2 |
| AB |
| AC |
| CA |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 3 |
| CD |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
| 1 |
| 6 |
| AD |
| AC |
| 1 |
| 2 |
| AB |
| 1 |
| 3 |
| AC |
| 1 |
| 6 |
| AC |
| AG |
| 1 |
| 2 |
| AB |
| 1 |
| 3 |
| AC |
| 1 |
| 6 |
| AD |
| 1 |
| 2 |
| AB |
| 1 |
| 3 |
| AC |
| 1 |
| 6 |
| AD |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 36 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 6 |
| 85 |
| 36 |
30
| ||
| 36 |
| AG |
| ||||
| 6 |


科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 12 |

查看答案和解析>>
科目:高中数学 来源: 题型:047
如图所示,设
a=(-l-x)i,b=(1-x)i+yj(x,y∈R,i,j分别是x、y轴正方向上的单位向量),且|a|=|b|.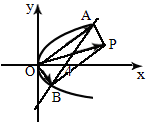
(1)
求点M(x,y)的轨迹C的方程;(2)
过点(4,0)作直线l交曲线C于A、B两点,设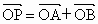 ,求证:四边形OAPB为矩形.
,求证:四边形OAPB为矩形.查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省实验中学高三(上)期末数学试卷(文科)(解析版) 题型:选择题
 的离心率,则计算机执行该运算后输出结果是( )
的离心率,则计算机执行该运算后输出结果是( )




查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省武汉市华中师大一附中高二(下)期中数学试卷(理科)(解析版) 题型:解答题
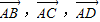 表示
表示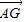
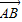 |=|
|=|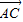 |=2,|
|=2,|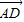 |=3,求|
|=3,求|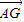 |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com