
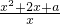 )>0恒成立,求实数a的取值范围.
)>0恒成立,求实数a的取值范围. >1,则题意得f(
>1,则题意得f( )>0
)>0 )>0
)>0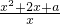 )>0=f(1)恒成立,即
)>0=f(1)恒成立,即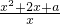 >1恒成立
>1恒成立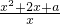 )>0转化为a>-x2-x在x∈[1,+∞)时恒成立,根据二次函数的性质,我们即可求出实数a的取值范围.
)>0转化为a>-x2-x在x∈[1,+∞)时恒成立,根据二次函数的性质,我们即可求出实数a的取值范围. ),(3)的关键是利用函数的单调性对不等式f(
),(3)的关键是利用函数的单调性对不等式f(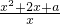 )>0进行变形.
)>0进行变形. 

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市西南师大附中高一(上)期中数学试卷(解析版) 题型:解答题
 是函数y=g(x) 图象上的点.
是函数y=g(x) 图象上的点.查看答案和解析>>
科目:高中数学 来源:2007年上海市徐汇区零陵中学高三3月综合练习数学试卷(五)(解析版) 题型:解答题
 上存在两个不同点关于直线y=x对称,求出其坐标;若曲线
上存在两个不同点关于直线y=x对称,求出其坐标;若曲线 (p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围;
(p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围; 及
及 加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间
加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间 上单调递减,在区间
上单调递减,在区间 上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)
上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:2.10 函数的最值(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com