已知圆C以(3,-1)为圆心,5为半径,过点S(0,4)作直线l与圆C交于不同两点A,B.
(Ⅰ)若AB=8,求直线l的方程;
(Ⅱ)当直线l的斜率为-2时,过直线l上一点P,作圆C的切线PT(T为切点)使PS=PT,求点P的坐标;
(Ⅲ)设AB的中点为N,试在平面上找一点M,使MN的长为定值.
【答案】
分析:(Ⅰ)当斜率不存在时,x=0符合条件; 当斜率存在时,设出直线的方程,再由圆心距的平方与弦长一半的平方等于半径的平方求得圆心距,最后由点到直线的距离公式求得l的方程.
(Ⅱ)当l斜率为-2时,直线l方程为y=-2x+4,有x
2+(y-4)
2=(x-3)
2+(y+1)
2-25,从而得到点P的坐标.
(Ⅲ)由直角三角形斜边上的中线等于斜边一半可得.
解答:解:(Ⅰ)圆心C坐标(3,-1),半径r=5,
由条件可知:圆心C到直线l的距离为3.(3分)
当斜率不存在时,x=0符合条件; (4分)
当直线l斜率存在时,设其为k,
则
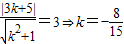
,
则直线l的方程为8x+15y-60=0.
综上,直线l方程是8x+15y-60=0或x=0;(6分)
(Ⅱ)知直线l方程为y=-2x+4,设点P(a,4-2a),
则由PC
2-r
2=PS
2得:a
2+4a
2=(a-3)
2+(5-2a)
2-25,

,
所求点P为
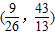
;(10分)
(Ⅲ)根据直角三角形斜边上的中线等于斜边一半有:
定点M的坐标为

.(16分)
点评:本题主要考查直线与圆的方程的应用,主要涉及了垂径定理,切线的性质及直角三角形的性质.当直线与圆相交时,常常过圆心作弦的垂线,根据弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.

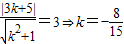 ,
, ,
,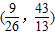 ;(10分)
;(10分) .(16分)
.(16分)

 阅读快车系列答案
阅读快车系列答案