对于数列{an},从第二项起,每一项与它前一项的差依次组成等比数列,称该等比数列为数列{an}的“差等比数列”,记为数列{bn}.设数列{bn}的首项b1=2,公比为q(q为常数).
(I)若q=2,写出一个数列{an}的前4项;
(II)(ⅰ)判断数列{an}是否为等差数列,并说明你的理由;
(ⅱ)a1与q满足什么条件,数列{an}是等比数列,并证明你的结论;
(III)若a1=1,1<q<2,数列{an+cn}是公差为q的等差数列(n∈N*),且c1=q,求使得cn<0成立的n的取值范围.
【答案】
分析:(Ⅰ)因为数列{b
n}是等比数列,且b
1=2,q=2,所以b
2=4,b
3=8,由此能够求出一个数列{a
n}的前4项.
(Ⅱ)(ⅰ)因为b
1=2,所以
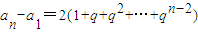
.q=1时,数列{a
n}是等差数列.若q≠1时,数列{a
n}不是等差数列.
(ⅱ)因为数列{b
n}是等比数列,首项b
1=2,公比为q,所以b
2=2q,
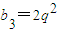
.所以a
2=a
1+2,a
3=a
1+2+2q.因为数列{a
n}是等比数列,所以
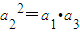
,所以当q=
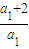
时,数列{a
n}是等比数列.
(Ⅲ)因为{a
n+c
n}是公差为q的等差数列,所以(a
n+c
n)-(a
n-1+c
n-1)=q,由此猜想:当n≥3时,c
n<0.再用数学归纳法证明.
解答:解:(Ⅰ)因为数列{b
n}是等比数列,且b
1=2,q=2,
所以b
2=4,b
3=8,
所以a
1=1,a
2=3,a
3=7,a
15=15.(写出满足条件的一组即可)
…(2分)
(Ⅱ)(ⅰ)因为b
1=2,
所以a
2-a
1=2,a
3-a
2=2q,
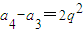
,…,
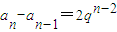
,n≥2.
所以
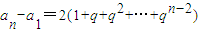
.
①若q=1,所以a
n-a
n-1=2,
所以数列{a
n}是等差数列.…(3分)
②若q≠1,所以
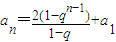
,
所以a
n+1-a
n=
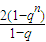
-
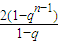
=
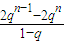
=2q
n-1.
因为q≠1,所以2q
n-1不是常数.
所以数列{a
n}不是等差数列.…(5分)
(ⅱ)因为数列{b
n}是等比数列,首项b
1=2,公比为q,
所以b
2=2q,
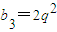
.所以a
2=a
1+2,a
3=a
1+2+2q.
因为数列{a
n}是等比数列,
所以
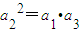
,
即(a
2+2)
2=a
1•(a
1+2+2q),
所以q=
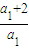
.
所以当q=
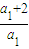
时,数列{a
n}是等比数列.…(7分)
(Ⅲ)因为{a
n+c
n}是公差为q的等差数列,
所以(a
n+c
n)-(a
n-1+c
n-1)=q,
又
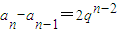
,
所以
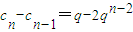
,
所以
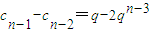
,…,c
3-c
2=q-2q,c
2-c
1=q-2,
所以
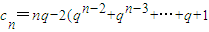
)
=nq-
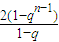
.…(9分)
所以c
1=q>0,c
2=2(q-1)>0,c
3=q-2<0,
c
4=-2(q
2-q+1)=-2(q-

)
2-

<0,…
猜想:当n≥3时,c
n<0.
用数学归纳法证明:
①当n=3时,c
3<0显然成立,
②假设当n=k(k≥3)时,c
k<0,
那么当n=k+1时,
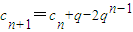
<q-2q
k-1=q(1-2q
k-2),
因为1<q<2,k≥3,
所以1-2q
k-2<0.
所以c
n+1<0,
所以当n=k+1时,c
n+1<0成立.
由①、②所述,当n≥3时,恒有c
n<0.…(14分)
点评:本题考查等差数列和等比数列的证明,综合性强,难度大,对数学思维的要求较高,解题时要认真审题,仔细解答,注意数学归纳法的合理运用.

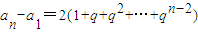 .q=1时,数列{an}是等差数列.若q≠1时,数列{an}不是等差数列.
.q=1时,数列{an}是等差数列.若q≠1时,数列{an}不是等差数列.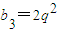 .所以a2=a1+2,a3=a1+2+2q.因为数列{an}是等比数列,所以
.所以a2=a1+2,a3=a1+2+2q.因为数列{an}是等比数列,所以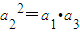 ,所以当q=
,所以当q=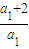 时,数列{an}是等比数列.
时,数列{an}是等比数列.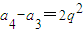 ,…,
,…,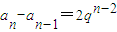 ,n≥2.
,n≥2.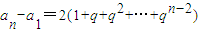 .
.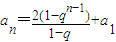 ,
,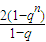 -
-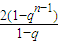 =
=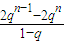 =2qn-1.
=2qn-1.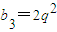 .所以a2=a1+2,a3=a1+2+2q.
.所以a2=a1+2,a3=a1+2+2q.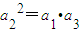 ,
,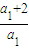 .
.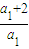 时,数列{an}是等比数列.…(7分)
时,数列{an}是等比数列.…(7分)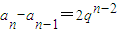 ,
,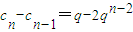 ,
,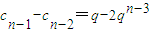 ,…,c3-c2=q-2q,c2-c1=q-2,
,…,c3-c2=q-2q,c2-c1=q-2,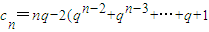 )
)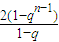 .…(9分)
.…(9分) )2-
)2- <0,…
<0,…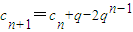 <q-2qk-1=q(1-2qk-2),
<q-2qk-1=q(1-2qk-2),

 智慧小复习系列答案
智慧小复习系列答案