
(本小题只理科做,满分14分)如图,已知 平面
平面 ,
,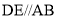 ,△
,△ 是正三角形,
是正三角形, ,且
,且 是
是 的中点.
的中点.

(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求平面 与平面
与平面 所成锐二面角的大小.
所成锐二面角的大小.
(1)见解析;(2)见解析;(3)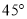 .
.
【解析】
试题分析:(1)取CE中点P,连接FP、BP,根据中位线定理可知FP||DE,且且FP= ,而AB||DE,且AB=
,而AB||DE,且AB= 则ABPF为平行四边形,则AF||BP,AF
则ABPF为平行四边形,则AF||BP,AF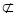 平面BCE,BP?平面BCE,满足线面平行的判定定理,从而证得结论;
平面BCE,BP?平面BCE,满足线面平行的判定定理,从而证得结论;
(2)根据AB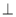 平面ACD,DE||AB,则DE
平面ACD,DE||AB,则DE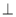 平面ACD,又AF?平面ACD,根据线面垂直的性质可知
平面ACD,又AF?平面ACD,根据线面垂直的性质可知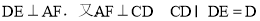 ,满足线面垂直的判定定理,证得AF
,满足线面垂直的判定定理,证得AF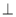 平面CDE,又BP||AF,则BP
平面CDE,又BP||AF,则BP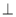 平面CDE,BP
平面CDE,BP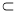 平面BCE,根据面面垂直的判定定理可证得结论;
平面BCE,根据面面垂直的判定定理可证得结论;
(3)由(2),以F为坐标原点,FA,FD,FP所在的直线分别为x,y,z轴建立空间直角坐标系F﹣xyz.设AC=2,根据线面垂直求出平面BCE的法向量n,而m=(0,0,1)为平面ACD的法向量,设平面BCE与平面ACD所成锐二面角为α,根据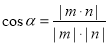 可求出所求.
可求出所求.

试题解析:(1)解:取CE中点P,连结FP、BP,
∵F为CD的中点,∴FP||DE,且FP=
又AB||DE,且AB= ∴AB||FP,且AB=FP,
∴AB||FP,且AB=FP,
∴ABPF为平行四边形,∴AF||BP
又∵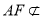 平面BCE,BP
平面BCE,BP 平面BCE,
平面BCE,
∴AF||平面BCE
(2)∵△ACD为正三角形,∴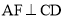 .
.
∵AB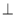 平面ACD,DE||AB,
平面ACD,DE||AB,
∴DE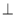 平面ACD,又AF
平面ACD,又AF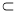 平面ACD,
平面ACD,
∴DE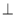 AF.又AF
AF.又AF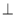 CD,CD∩DE=D,
CD,CD∩DE=D,
∴AF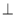 平面CDE
平面CDE
又BP||AF,∴BP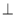 平面CDE.又∵BP
平面CDE.又∵BP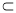 平面BCE,
平面BCE,
∴平面BCE⊥平面CDE
(3)法一、由(2),以F为坐标原点,
FA,FD,FP所在的直线分别为x,y,z轴(如图),

建立空间直角坐标系F—xyz.设AC=2,
则C(0,—1,0),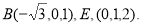
设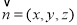 为平面BCE的法向量,
为平面BCE的法向量, 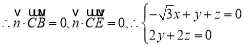 ,令n=1,则
,令n=1,则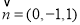
显然,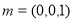 为平面ACD的法向量.
为平面ACD的法向量.
设面BCE与面ACD所成锐二面角为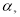
则

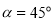 .
.
即平面BCE与平面ACD所成锐二面角为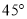
法二、延长EB、DA,设EB、DA交于一点O,连结CO.
则面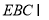 面
面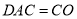 .
.
由AB是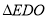 的中位线,则
的中位线,则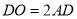 .
.
在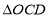 中
中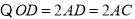 ,
,  .
. 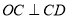 ,又
,又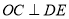 .
. 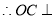 面
面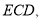 而CE
而CE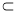 面ECD,
面ECD,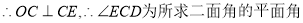
在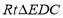 中,
中,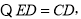
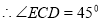
即平面BCE与平面ACD所成锐二 面角为
面角为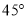 .
.
考点:与二面角有关的立体几何综合题;直线与平面平行的判定;平面与平面垂直的判定.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源:2014-2015学年湖南省益阳市高二9月月考文科数学试卷(解析版) 题型:选择题
已知椭圆G的中心在坐标原点,长轴在 轴上,离心率为
轴上,离心率为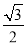 ,且椭圆
,且椭圆 上一点到其两个焦点的距离之和为12,则椭圆
上一点到其两个焦点的距离之和为12,则椭圆 的方程为( )
的方程为( )
A..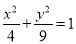 B.
B. C.
C.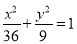 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省高一上学期阶段考试数学试卷(解析版) 题型:填空题
已知集合 ,且
,且 是从集合A到B的一个映射,若集合
是从集合A到B的一个映射,若集合 中的元素
中的元素 与集合
与集合 中的元素3对应,则
中的元素3对应,则 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北鄂州泽林中学高二上第一次月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以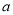 表示.
表示.
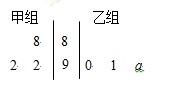
(1)若甲、乙两个小组的数学平均成绩相同,求 的值;
的值;
(2)当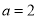 时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北鄂州泽林中学高二上第一次月考理科数学试卷(解析版) 题型:选择题
将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场做的9个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以 表示:
表示:
则7个剩余分数的方差为( )
A. B .
B . C.36 D.
C.36 D. 
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北襄阳襄州一中等四校高二上学期期中文科数学试卷(解析版) 题型:选择题
如图所示是四棱锥的三视图,则该几何的体积等于( )
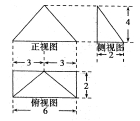
A.16 B.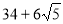 C.6 D.
C.6 D.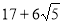
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com