
分析 实数a,b,c成等比数列,设公比为q,则a=$\frac{b}{q}$,c=bq.又a+b+c=4,可得b=$\frac{4}{\frac{1}{q}+q+1}$.当q>0时,$0<b≤\frac{4}{3}$.当q<0时,0>b≥-4.即可得出a+c=4-b的取值范围.
解答 解:实数a,b,c成等比数列,设公比为q,
则a=$\frac{b}{q}$,c=bq.
又a+b+c=4,
∴$\frac{b}{q}$+b+bq=4,
∴b=$\frac{4q}{1+q+{q}^{2}}$=$\frac{4}{\frac{1}{q}+q+1}$.
当q>0时,$0<b≤\frac{4}{3}$,当且仅当q=1时取等号.
当q<0时,0>b≥-4,当且仅当q=-1时取等号.
∴a+c=4-b,
∴当q>0时,(a+c)∈[$\frac{8}{3}$,4);
当q<0时,(a+c)∈(4,8].
则a+c的取值范围是[$\frac{8}{3}$,4)∪(4,8].
故答案为:[$\frac{8}{3}$,4)∪(4,8].
点评 本题考查了等比数列的性质、基本不等式的性质,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2-2i | B. | -2-2i | C. | -2+2i | D. | 2+2i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
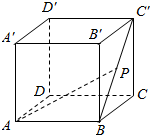 如图,ABCD-A′B′C′D′是棱长为1的正方体,点P是BC′上的动点,$\overrightarrow{BP}=λ\overrightarrow{BC'}$,则$\overrightarrow{AP}•\overrightarrow{DC}$的值是1.
如图,ABCD-A′B′C′D′是棱长为1的正方体,点P是BC′上的动点,$\overrightarrow{BP}=λ\overrightarrow{BC'}$,则$\overrightarrow{AP}•\overrightarrow{DC}$的值是1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com