已知函数f (x)＝lg(ax－bx)(a >1，0< b<1)
(1) 求f (x)
的定义域；
(2) 此函数的图象上是否存在两点，过这两点的直线平行于x轴？
(3) 当a、b满足什么条件时f (x)恰在(1，＋∞)取正值
科目：高中数学 来源： 题型：解答题
某品牌电视生产厂家有A、B两种型号的电视机参加了家电下乡活动，若厂家A、B对两种型号的电视机的投放金额分别为p、q万元，农民购买电视机获得的补贴分别为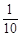
p、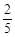
lnq万元，已知A、B两种型号的电视机的投放总额为10万元，且A、B两种型号的电视机的投放金额均不低于1万元，请你制定一个投放方案，使得在这次活动中农民得到的补贴最多，并求出最大值(精确到0.1，参考数据：
)．
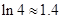查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：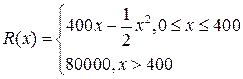
，其中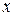
是仪器的月产量．
(1) 将利润表示为月产量的函数
；
(2) 当月产量为何值时，公司所获利润最大？最大利润为多少元(总收益=总成本+利润) ？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）已知幂函数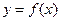
的图象经过点
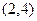，对于偶函数
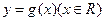，当
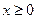时，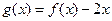
。
（1）求函数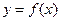的解析式；
（2）求当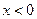
时，函数
的解析式，并在给定坐标系下，画出函数 的图象
（3）写出函数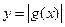
的单调递减区间
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本大题12分）已知二次函数．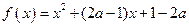
（1）判断命题：“对于任意的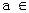
R（R为实数集），方程
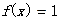必有实数根”的真假，并写出判断过程
（2），若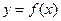
在区间
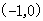及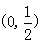
内各有一个零点．求实数a的范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
在定义域内单调递增，故不存在所述两点。
单调递增，
且对任意实数
均有
成立，求
表达式；
时，
是单调函数，求实数
的取值范围。
满足不等式
，求函数
(
)的最小
值．
.
的值域G；
，不等式
恒成立，求实数
的取值范围.
的解集为
；
的值；
在
上恒成立，求实数
的最大值.