
解析:根据题意:4x+y+6=0,3x-5y-6=0两条直线在y轴上的截距互为相反数,∴斜率存在.
解法一:设所求方程为y=kx,代入两直线
4x+y+6=0,3x-5y-6=0,∴4x+kx+6=0,x1=-![]() ;3x-5kx-6=0,x2=
;3x-5kx-6=0,x2=![]()
∴x1+x2=0![]() k=-
k=-![]() ∴l:x+6y=0.
∴l:x+6y=0.
解法二:设M、N两点在所求直线上,且M、N关于原点对称,
M点坐标为(x0,y0),∴N(-x0,-y0),?
M在4x+y+6=0上,N在3x-5y-6=0上.?
∴4x0+y0+6=0①,-3x0+5y0-6=0②.?
∵M、N关于原点对称,∴所求直线过原点.?
①+②得x0+6y0=0,∴所求直线为x+6y=0.
解法三:设y=kx,
由(4x+y+6)(3x-5y-6)=0,?
∴(4x+kx+6)(3x-5kx-6)=0,(5k2+17k-12)x2-6(6k+1)x+6=0,?
Δ=36(36k2+12k+1)-24(5k2+17k-12)≥0,?
98k2+2k+27≥0,恒大于0.?
![]()
∴l:x+6y=0.
解法四:设直线的参数式为
∴4tcosα+tsinα+6=0,![]()
3tcosα-5tsinα-6=0,![]()
∵两点关于原点对称,∴t1+t2=0.?
∴5sinα-3cosα+4cosα+sinα=0?tanα=-![]() .?
.?
∴l:x+6y=0.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| lim |
| x→1 |
| x2+b |
| x-1 |
查看答案和解析>>
科目:高中数学 来源:高考总复习全解 数学 一轮复习·必修课程 (人教实验版) B版 人教实验版 B版 题型:044
过点M(0,1)作直线l,使它被两条已知直线l1:x-3y+10=0和l2:2x+y-8=0所截得的线段AB被点M平分.求直线的方程.
查看答案和解析>>
科目:高中数学 来源:2010年山西省太原二中高考数学二模试卷(解析版) 题型:解答题
 ,
, 为一平面内两非零向量,则
为一平面内两非零向量,则 ⊥
⊥ 是|
是| +
+ |=|
|=| -
- |的充要条件;
|的充要条件; =2,则b=-1.
=2,则b=-1.查看答案和解析>>
科目:高中数学 来源:2010年高考数学综合训练试卷(04)(解析版) 题型:解答题
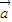 ,
,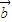 为一平面内两非零向量,则
为一平面内两非零向量,则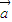 ⊥
⊥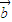 是|
是|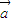 +
+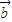 |=|
|=|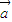 -
-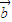 |的充要条件;
|的充要条件;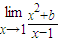 =2,则b=-1.
=2,则b=-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com