
���� ��1�����Բ��O���꣬��O��M����ֱ��x+y+2=0�Գƣ������е����깫ʽ��б�ʵĹ�ϵ�г���ϵʽ���������a��b��ֵ������ԲO����A��ȷ����ԲO���̼��ɣ�
��2����Բ��O��ֱ��EF��GH�ľ���ֱ�Ϊd1��d2����d12+d22=|ON|2����N�������d12+d22��ֵ����ʾ��|EF|��|GH|��������ʾ��S�����û�������ʽ������ֵ���ɣ�
��3��ֱ��CD�����㣬��������Ϊ��$\frac{1}{2}$��-1��������Ϊ��������ɵã�O��P��C��D�ĵ㹲Բ������OPΪֱ����Բ�ϣ����P���꣬��ʾ����OPΪֱ����Բ����ԲO���̽��ȷ����ֱ��CD���̣����ɵõ�ֱ��CD����Ķ������꣮
��� �⣺��1����Բ��O��a��b������������ã�$\left\{\begin{array}{l}{\frac{a-2}{2}+\frac{b-2}{2}+2=0}\\{\frac{b+2}{a+2}=1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=0}\\{b=0}\end{array}\right.$��
��ԲO����Ϊx2+y2=r2��
��A��1��1������ã�r2=2����ԲO����Ϊx2+y2=2��
��2����Բ��O��ֱ��EF��GH�ľ���ֱ�Ϊd1��d2����d12+d22=|ON|2=$\frac{3}{2}$��
��|EF|=2$\sqrt{{r}^{2}-{{d}_{1}}^{2}}$=2$\sqrt{2-{{d}_{1}}^{2}}$��|GH|=2$\sqrt{{r}^{2}-{{d}_{2}}^{2}}$=2$\sqrt{2-{{d}_{2}}^{2}}$��
���ҽ���2-d12=2-d22����d1=d2=$\frac{\sqrt{3}}{2}$ʱȡ�Ⱥţ�
��S=$\frac{1}{2}$|EF|•|GH|=2$\sqrt{��2-{{d}_{1}}^{2}����2-{{d}_{2}}^{2}��}$��2-d12+2-d22=4-$\frac{3}{2}$=$\frac{5}{2}$��
���ı���EGFH��������ֵΪ$\frac{5}{2}$��
��3��ֱ��CD�����㣬��������Ϊ��$\frac{1}{2}$��-1��������Ϊ��
������ɵã�O��P��C��D�ĵ㹲Բ������OPΪֱ����Բ�ϣ�
��P��t��$\frac{1}{2}$t-2�����䷽��Ϊx��x-t��+y��y-$\frac{1}{2}$t+2��=0����x2-tx+y2-��$\frac{1}{2}$t-2��y=0�٣�
��C��D��ԲO��x2+y2=2�Ϣڣ�
��-�ٵã�ֱ��CD�ķ���Ϊtx+��$\frac{1}{2}$t-2��y-2=0������x+$\frac{y}{2}$��t-2y-2=0��
��$\left\{\begin{array}{l}{x+\frac{y}{2}=0}\\{2y+2=0}\end{array}\right.$����$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-1}\end{array}\right.$��
��ֱ��CD�����㣨$\frac{1}{2}$��-1����
���� ���⿼����ֱ����Բ�ķ��̵�Ӧ�ã��漰��֪ʶ�У�Բ�ı����̣������ľ��빫ʽ����������ʽ�����ã��Լ���������ֱ�߷��̣��������չ�ʽ�������ǽⱾ��Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 6�� | C�� | 4�� | D�� | $\frac{��}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
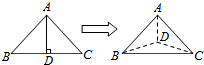 ��ͼ���Ե���ֱ��������ABC��б��BC�ϵĸ�ADΪ�ۺۣ��ѡ�ABD�͡�ACD��
��ͼ���Ե���ֱ��������ABC��б��BC�ϵĸ�ADΪ�ۺۣ��ѡ�ABD�͡�ACD��| A�� | �٢ڢ� | B�� | �٢ڢ� | C�� | �ڢۢ� | D�� | �٢ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 1��2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{4}{9}$ | B�� | $\frac{1}{9}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com