
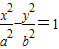 的离心率为e.
的离心率为e.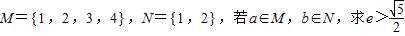 的概率;
的概率;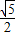 的概率.
的概率.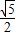 ”对应
”对应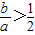 ,符合条件的有(3,1),(4,1)两种情况,用随机事件的概率公式,可得所求的概率;
,符合条件的有(3,1),(4,1)两种情况,用随机事件的概率公式,可得所求的概率;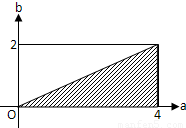 解:(1)从M任取一数为a,从N中任取一数为b,有(1,1),(1,2),
解:(1)从M任取一数为a,从N中任取一数为b,有(1,1),(1,2),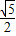 ”,则
”,则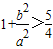 ,
,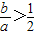 ,符合条件的有(3,1),(4,1)两种情况,
,符合条件的有(3,1),(4,1)两种情况,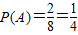
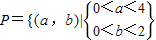 ,P对应的图形是长为4,宽为2的长方形区域(如图),其面积S1=8,
,P对应的图形是长为4,宽为2的长方形区域(如图),其面积S1=8,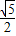 },则a<2b,满足条件的点(a,b)位于图中阴影部分,其面积S2=4,
},则a<2b,满足条件的点(a,b)位于图中阴影部分,其面积S2=4,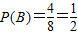
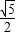 的概率,着重考查了双曲线的离心率和随机事件的概率等知识点,属于基础题.
的概率,着重考查了双曲线的离心率和随机事件的概率等知识点,属于基础题. 

 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:2010-2011学年河北省高三下学期开学考试数学文卷 题型:选择题
已知双曲线 的离心率为e,左、右两焦点分别为F1、F2,焦距为
的离心率为e,左、右两焦点分别为F1、F2,焦距为 ,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 (
)
,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 (
)
A. B. 3 C. D.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省高三下学期开学考试数学文卷 题型:选择题
已知双曲线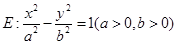 的离心率为e,左、右两焦点分别为F1、F2,焦距为
的离心率为e,左、右两焦点分别为F1、F2,焦距为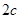 ,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 (
)
,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 (
)
A. B. 3 C. D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
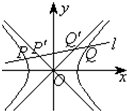 已知双曲线
已知双曲线 的离心率为e,右顶点为A,左、右焦点分别为F1、F2,点E为右准线上的动点,∠AEF2的最大值为θ.
的离心率为e,右顶点为A,左、右焦点分别为F1、F2,点E为右准线上的动点,∠AEF2的最大值为θ.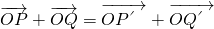 .
.查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省衡水市冀州中学高三(下)开学数学试卷(文科)(解析版) 题型:选择题
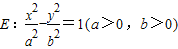 的离心率为e,左、右两焦点分别为F1、F2,焦距为2c,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为( )
的离心率为e,左、右两焦点分别为F1、F2,焦距为2c,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为( )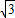
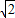
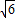
查看答案和解析>>
科目:高中数学 来源:2009-2010学年四川省南充一中高三(下)6月适应性考试数学试卷(理科)(解析版) 题型:解答题
 的离心率为e,右顶点为A,左、右焦点分别为F1、F2,点E为右准线上的动点,∠AEF2的最大值为θ.
的离心率为e,右顶点为A,左、右焦点分别为F1、F2,点E为右准线上的动点,∠AEF2的最大值为θ. .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com