
| 1 |
| 2 |
| 1 |
| 2 |
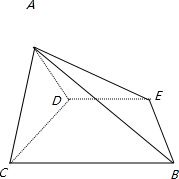
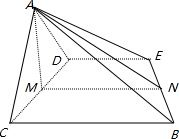 证明:取BE的中点M,CD的中点N,连接 AM,AN,MN,
证明:取BE的中点M,CD的中点N,连接 AM,AN,MN,

科目:高中数学 来源:2014届河南省毕业班阶段测试一理数学卷(解析版) 题型:解答题
如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE, =45
=45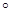 ,O是BC的中点,AO=
,O是BC的中点,AO= ,且BC=6,AD=AE=2CD=2
,且BC=6,AD=AE=2CD=2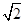 ,
,
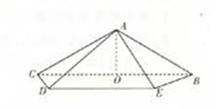
(1)证明:AO⊥平面BCD;(2)求二面角A-CD-B的平面角的正切值.
查看答案和解析>>
科目:高中数学 来源:2014届河南省毕业班阶段测试一文数学卷(解析版) 题型:解答题
如图,在四棱锥A-BCDE中,侧面∆ADE是等边三角形,底面BCDE是等腰梯形,且CD∥BE,DE=2,CD=4,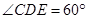 ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,
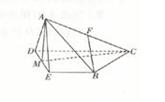
求证:(1)平面ADE⊥平面BCD;
(2)FB∥平面ADE.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三适应性考试理科数学 题型:解答题
(本小题满分12分)
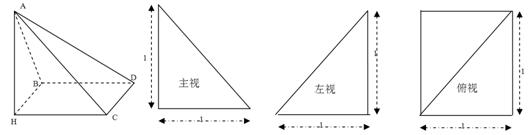
如图示,在四棱锥A-BHCD中,AH⊥面BHCD,此棱锥的三视图如下:
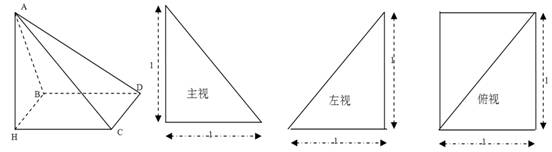
(1)求二面角B-AC-D的大小;
(2)在线段AC上是否存在一点E,使ED与面BCD成45°角?若存在,确定E的位置;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三12月月考数学理卷 题型:解答题
(本小题满分12分)
如左图示,在四棱锥A-BHCD中,AH⊥面BHCD,此棱锥的三视图如下:
(1)求二面角B-AC-D的大小;
(2)在线段AC上是否存在一点E,使ED与面BCD成45°角?若存在,确定E的位置;若不存在,说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com