
、函数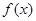 的定义域为D,若对于任意
的定义域为D,若对于任意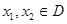 ,当
,当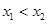 时,都有
时,都有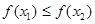 ,则称函数
,则称函数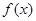 在D上为非减函数.设函数
在D上为非减函数.设函数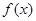 为定义在[0,1]上的非减函数,且满足以下三个条件:
为定义在[0,1]上的非减函数,且满足以下三个条件:
① 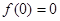 ;②
;② 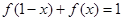
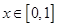 ;
③ 当
;
③ 当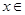
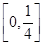 时,
时,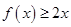 恒成立.则
恒成立.则 .
.
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
| a |
| 2 |
| b |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三下学期第二次联考文数学试卷(解析版) 题型:选择题
设函数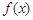 的定义域为D,如果
的定义域为D,如果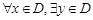 ,使
,使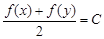 (C为常数
(C为常数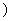 成立,则称函数
成立,则称函数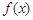 在D上的均值为C. 给出下列四个函数:①
在D上的均值为C. 给出下列四个函数:①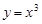 ;②
;②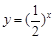 ;③
;③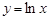 ;④
;④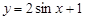 ,则满足在其定义域上均值为1的函数的个数是(
)
,则满足在其定义域上均值为1的函数的个数是(
)
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省瓦房店市五校高二上学期竞赛数学理卷 题型:选择题
函数 的定义域为D,若对于任意x1,x2∈D,当x1<x2时,都有
的定义域为D,若对于任意x1,x2∈D,当x1<x2时,都有 ≤
≤ ,
,
则称函数 在D上为非减函数.设函数
在D上为非减函数.设函数 在[0,1]上为非减函数,且满足以下三个条件:①
在[0,1]上为非减函数,且满足以下三个条件:① ; ②
; ② ③
③
则 +
+ 等于 ( )
等于 ( )
A. B.
B. C.1 D.
C.1 D.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省厦门市高三上学期末理科数学卷 题型:选择题
设函数 的定义域为D,若存在非零实数h使得对于任意
的定义域为D,若存在非零实数h使得对于任意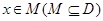 ,有
,有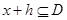 ,且
,且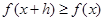 ,则称
,则称 为M上的“h阶高调函数”。给出如下结论:
为M上的“h阶高调函数”。给出如下结论:
①若函数 在R上单调递增,则存在非零实数h使
在R上单调递增,则存在非零实数h使 为R上的“h阶高调函数”;
为R上的“h阶高调函数”;
②若函数 为R上的“h阶高调函数”,则
为R上的“h阶高调函数”,则 在R上单调递增;
在R上单调递增;
③若函数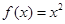 为区间
为区间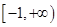 上的“h阶高诬蔑财函数”,则
上的“h阶高诬蔑财函数”,则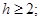
④若函数 在R上的奇函数,且
在R上的奇函数,且 时,
时,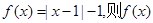 只能是R上的“4阶高调函数”。
只能是R上的“4阶高调函数”。
其中正确结论的序号为 ( )
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com