练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖騰.在如下图所示的阳马P-ABCD中，侧棱底面ABCD，且，则当点E在下列四个位置：PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中，鳖臑有( )

    A.1个B.2个C.3个D.4个

    【答案】C

    【解析】

    四个面都是直角三角形的四面体中必有棱与面垂直，由此可得．

    结合图形知阳马P-ABCD中只有四面体和是鳖臑，

    若为中点，如图，与类比知的四个面都是直角三角形，是鳖臑，

    若是中点，如图，由于，∴，另外由与底面垂直得与垂直，从而可得与平面垂直，即得，由线面垂直判定定理得平面，从而，那么的四个面都是直角三角形，此时是鳖臑，

    同理是中点时，也是鳖臑，

    当是中点时，不是直角三角形，不是鳖臑，

    因此鳖臑有3个．

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设A是圆O：x2+y2＝16上的任意一点，l是过点A且与x轴垂直的直线，B是直线l与x轴的交点，点Q在直线l上，且满足4|BQ|＝3|BA|．当点A在圆O上运动时，记点Q的轨迹为曲线C．

    （1）求曲线C的方程；

    （2）已知直线y＝kx﹣2（k≠0）与曲线C交于M，N两点，点M关于y轴的对称点为M′，设P（0，﹣2），证明：直线M′N过定点，并求△PM′N面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知且，设命题函数在R上单调递减，命题对任意实数x，不等式恒成立.

    （1）求非q为真时，实数c的取值范围；

    （2）如果命题为真命题，且为假命题，求实数c的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    (1)若，求的最大值；

    (2)若恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的定义域；

    （2）若函数的最小值为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，曲线在点处的切线方程为.

    （1）求的解析式；

    （2）证明：曲线上任一点处的切线与直线和直线所围成的三角形面积为定值，并求此定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的方程为，过点的一条直线与抛物线交于两点，若抛物线在两点的切线交于点.

    （1）求点的轨迹方程；

    （2）设直线与直线的夹角为，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若在处的切线方程为，求的值；

    （2）若为区间上的任意实数，且对任意，总有成立，求实数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

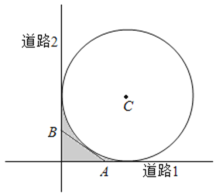
    【题目】如图，某城市有一块半径为（单位：百米）的圆形景观，圆心为，有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处图中阴影部分只有一块绿化地，后来有众多市民建议在绿化地上建一条小路，便于市民快捷地往返两条道路.规划部门采纳了此建议，决定在绿化地中增建一条与圆相切的小道问：两点应选在何处可使得小道最短？

    查看答案和解析>>

    同步练习册答案