Question

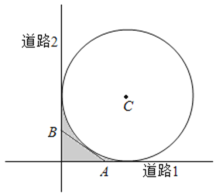
【题目】如图，某城市有一块半径为（单位：百米）的圆形景观，圆心为，有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处图中阴影部分只有一块绿化地，后来有众多市民建议在绿化地上建一条小路，便于市民快捷地往返两条道路.规划部门采纳了此建议，决定在绿化地中增建一条与圆相切的小道问：两点应选在何处可使得小道最短？

Answer 1

【答案】当两点离道路的交点都为（百米）时，小道最短

【解析】

分别由两条道路所在直线建立直角坐标系，设，，求得直线的方程和圆的方程，运用直线和圆相切的条件：，求得的关系，再由两点的距离公式和基本不等式，解不等式可得的最小值，以及此时的位置.

解：如图，分别由两条道路所在直线建立直角坐标系xOy.

设，，

则直线方程为，即.

因为与圆相切，所以

化简得，即

因此

因为，，所以

于是

又

解得，或

因为，所以

所以

当且仅当时取等号

所以最小值为，此时

答：当两点离道路的交点都为（百米）时，小道最短