
 (单位:度)与气温
(单位:度)与气温 (单位:
(单位: )之间的关系,随机统计了某
)之间的关系,随机统计了某 天的用电量与当天气温,并制作了对照表:
天的用电量与当天气温,并制作了对照表: |  |  |  |  | ||||
 |  |  |  |  | ||||
 ,当气温不低于
,当气温不低于 时,预测用电量最多为 度.
时,预测用电量最多为 度. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:填空题
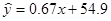

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
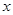 和年收入
和年收入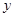 (万元),有以下的统计数据:
(万元),有以下的统计数据: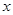 | 3 | 4 | 5 | 6 |
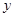 | 2.5 | 3 | 4 | 4.5 |
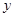 关于
关于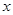 的线性回归方程
的线性回归方程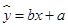 ;
;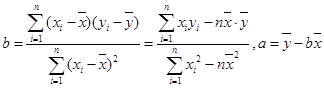 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,据此可以预测这个孩子10岁时的身高,则正确的叙述是( )
,据此可以预测这个孩子10岁时的身高,则正确的叙述是( ) | A.身高一定是145.83cm | B.身高超过146.00cm |
| C.身高低于145.00cm | D.身高在145.83cm左右 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x | 1.99 | 3 | 4 | 5.1 | 6.12 |
| y | 1.5 | 4.04 | 7.5 | 12 | 18.01 |
 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 转速χ(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
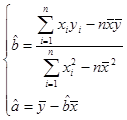
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
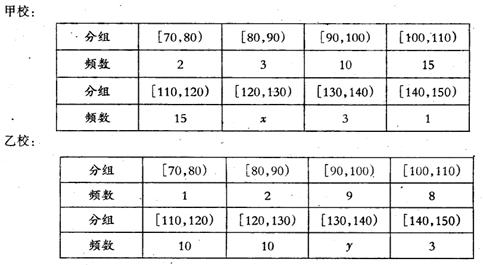
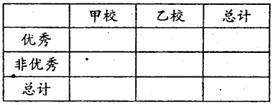
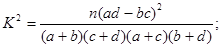
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
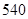 名
名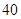 岁以上的人进行了调查,结果是:患胃病者生活不规律的共
岁以上的人进行了调查,结果是:患胃病者生活不规律的共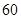 人,患胃病者生活规律的共
人,患胃病者生活规律的共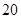 人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共
人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共 人.
人.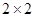 列联表.
列联表.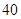 岁以上的人患胃病与否和生活规律是否有关。
岁以上的人患胃病与否和生活规律是否有关。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com