

科目:高中数学 来源:不详 题型:解答题
| | 积极参加班级工作 | 不太主动参加班级工作 |
| 学习积极性高 | 18 | 7 |
| 学习积极性一般 | 6 | 19 |
P( ≥k) ≥k) | 0.050 | 0.010 | 0.001 |  = = |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x y | y 1 | y 2 | 合计 |
| x1 | a | 21 | 73 |
| x2 | 2 | 25 | 27 |
| 合计 | b | 46 | 100 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 =60+90x,下列判断正确的是( )
=60+90x,下列判断正确的是( )| A.劳动产值为1 000元时,工资为50元 |
| B.劳动产值提高1 000元时,工资提高150元 |
| C.劳动产值提高1 000元时,工资提高90元 |
| D.劳动产值为1 000元时,工资为90元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.变量x与y正相关,u与v正相关 |
| B.变量x与y正相关,u与v负相关 |
| C.变量x与y负相关,u与v正相关 |
| D.变量x与y负相关,u与v负相关 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 商店名称 | A | B | C | D | E |
销售额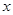 (千万元) (千万元) | 3 | 5 | 6 | 7 | 9 9 |
利润额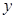 (百万元) (百万元) | 2 | 3 | 3 | 4 | 5 |
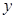 关于销售额
关于销售额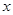 的回归直线方程;
的回归直线方程;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
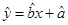 ;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。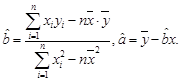 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工时间y(小时) | 2.5 | 3 | 4 | 4.5 |
 关于
关于 的线性回归方程
的线性回归方程 ;
; ,
, ,
,
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 (单位:度)与气温
(单位:度)与气温 (单位:
(单位: )之间的关系,随机统计了某
)之间的关系,随机统计了某 天的用电量与当天气温,并制作了对照表:
天的用电量与当天气温,并制作了对照表: |  |  |  |  | ||||
 |  |  |  |  | ||||
 ,当气温不低于
,当气温不低于 时,预测用电量最多为 度.
时,预测用电量最多为 度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com