
定义平面向量之间的一种运算“⊙”如下:对任意的a=(m,n),b=(p,q),令a⊙b= mq-np,下面说法错误的是 A.若a与b共线,则a⊙b =0 B.a⊙b =b⊙a
C.对任意的 R,有(
R,有(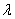 a)⊙b =
a)⊙b =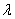 (a⊙b) D.(a⊙b)2+(a·b)2= |a|2|b|2
(a⊙b) D.(a⊙b)2+(a·b)2= |a|2|b|2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com