
【题目】已知函数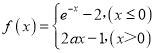 (a是常数且a>0).对于下列命题:
(a是常数且a>0).对于下列命题:
①函数f(x)的最小值是-1;
②函数f(x)在R上是单调函数;
③若f(x)>0在![]() 上恒成立,则a的取值范围是a>1;
上恒成立,则a的取值范围是a>1;
④对任意的x1<0,x2<0且x1≠x2,恒有
![]() .
.
其中正确命题的序号是____________.
科目:高中数学 来源: 题型:
【题目】给出下列四个命题
①四面体![]() 中,
中,![]() ,
,![]() ,则
,则![]()
②已知双曲线![]() 的两条渐近线的夹角为
的两条渐近线的夹角为![]() ,则双曲线的离心率为2
,则双曲线的离心率为2
③若正数![]() 和
和![]() 满足
满足![]() ,则
,则![]()
④向量![]() ,若存在实数
,若存在实数![]() ,使得
,使得![]() ,则
,则![]()
其中真命题的序号是______(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 经过点
经过点![]() ,且与极轴所成的角为
,且与极轴所成的角为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高三年级100名学生的视力情况进行统计(如果两眼视力不同,取较低者统计),得到如图所示的频率分布直方图,已知从这100人中随机抽取1人,其视力在![]() 的概率为
的概率为![]() .
.
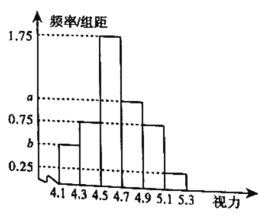
(1)求a,b的值;
(2)若报考高校A专业的资格为:任何一眼裸眼视力不低于5.0,已知在![]() 中有
中有![]() 的学生裸眼视力不低于5.0.现用分层抽样的方法从
的学生裸眼视力不低于5.0.现用分层抽样的方法从![]() 和
和![]() 中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年6月14日,世界杯足球赛在俄罗斯拉开帷幕,世界杯给俄罗斯经济带来了一定的增长,某纪念商品店的销售人员为了统计世界杯足球赛期间商品的销售情况,随机抽查了该商品商店某天200名顾客的消费金额情况,得到如图频率分布表:将消费顾客超过4万卢布的顾客定义为”足球迷”,消费金额不超过4万卢布的顾客定义为“非足球迷”。
消费金额/万卢布 |
|
|
|
|
|
| 合计 |
顾客人数 | 9 | 31 | 36 | 44 | 62 | 18 | 200 |
(1)求这200名顾客消费金额的中位数与平均数(同一组中的消费金额用该组的中点值作代表;
(2)该纪念品商店的销售人员为了进一步了解这200名顾客喜欢纪念品的类型,采用分层抽样的方法从“非足球迷”,“足球迷”中选取5人,再从这5人中随机选取3人进行问卷调查,则选取的3人中“非足球迷”人数的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】最近几年汽车金融公司发展迅猛,主要受益于监管层面对消费进人门槛的降低,互联网信贷消费的推广普及,以及汽车销售市场规模的扩张.如图是2013﹣2017年汽车金融行业资产规模统计图(单位:亿元).
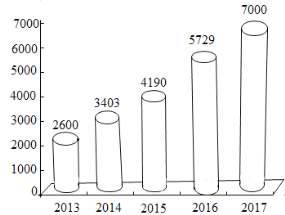
(1)以年份值2013,2014,…为横坐标,汽车金融行业资产规模(单位:亿元)为纵坐标,求y关于x的线性回归方程;
(2)利用(1)中的回归方程,预计2018年汽车金融行业资产规模(精确到亿元).
附:回归直线的斜率和截距的最小二乘估计公式分别为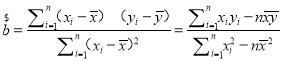 ,
,![]() (其中
(其中![]() ,
,![]() 为样本平均值).
为样本平均值).
参考数据:![]() 4.620×107,2015
4.620×107,2015![]() 4.619×107.
4.619×107.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业要设计制造一批大小、规格相同的长方体封闭水箱,已知每个水箱的表面积为432(每个水箱的进出口所占面积与制作材料的厚度均忽略不计).每个长方体水箱的底面长是宽的2倍.现设每个长方体水箱的底面宽是![]() ,用
,用![]() 表示每个长方体水箱的容积.
表示每个长方体水箱的容积.
(1)试求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)当![]() 为何值时,
为何值时,![]() 有最大值,并求出最大值.
有最大值,并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com