
【题目】最近几年汽车金融公司发展迅猛,主要受益于监管层面对消费进人门槛的降低,互联网信贷消费的推广普及,以及汽车销售市场规模的扩张.如图是2013﹣2017年汽车金融行业资产规模统计图(单位:亿元).
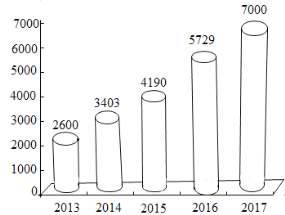
(1)以年份值2013,2014,…为横坐标,汽车金融行业资产规模(单位:亿元)为纵坐标,求y关于x的线性回归方程;
(2)利用(1)中的回归方程,预计2018年汽车金融行业资产规模(精确到亿元).
附:回归直线的斜率和截距的最小二乘估计公式分别为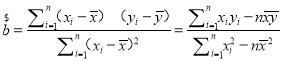 ,
,![]() (其中
(其中![]() ,
,![]() 为样本平均值).
为样本平均值).
参考数据:![]() 4.620×107,2015
4.620×107,2015![]() 4.619×107.
4.619×107.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数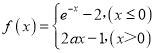 (a是常数且a>0).对于下列命题:
(a是常数且a>0).对于下列命题:
①函数f(x)的最小值是-1;
②函数f(x)在R上是单调函数;
③若f(x)>0在![]() 上恒成立,则a的取值范围是a>1;
上恒成立,则a的取值范围是a>1;
④对任意的x1<0,x2<0且x1≠x2,恒有
![]() .
.
其中正确命题的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,f(x)=lnx-ax,若函数在定义域上有且仅有4个零点,则实数a的取值范围是( )
A.(e,+∞)B.(0,![]() )
)
C.(1,![]() )D.(-∞,
)D.(-∞,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,已知椭圆的长轴为
的左、右焦点,已知椭圆的长轴为![]() 是椭圆
是椭圆![]() 上一动点,
上一动点,![]() 的最大值为
的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 上一点,
上一点,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,其中
,其中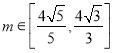 ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在南北方向有一条公路,一半径为100![]() 的圆形广场(圆心为
的圆形广场(圆心为![]() )与此公路所在直线
)与此公路所在直线![]() 相切于点
相切于点![]() ,点
,点![]() 为北半圆弧(弧
为北半圆弧(弧![]() )上的一点,过点
)上的一点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,计划在
,计划在![]() 内(图中阴影部分)进行绿化,设
内(图中阴影部分)进行绿化,设![]() 的面积为
的面积为![]() (单位:
(单位:![]() ),
),
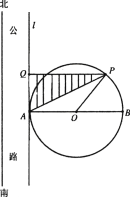
(1)设![]() ,将
,将![]() 表示为
表示为![]() 的函数;
的函数;
(2)确定点![]() 的位置,使绿化面积最大,并求出最大面积.
的位置,使绿化面积最大,并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)若![]() ,
,![]() ,证明
,证明![]() ;
;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上有两个零点?若存在,求出
上有两个零点?若存在,求出![]() 的取值范围:若不存在,请说明理由.
的取值范围:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,以此类推,已知2016年为丙申年,那么到改革开放100年时,即2078年为________年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() 是正三角形,
是正三角形,![]() 为
为![]() 的中点,平面
的中点,平面![]() 平面
平面![]() .
.
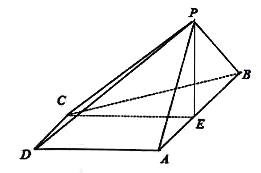
(1)求证:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com