
【题目】设函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)若![]() ,
,![]() ,证明
,证明![]() ;
;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上有两个零点?若存在,求出
上有两个零点?若存在,求出![]() 的取值范围:若不存在,请说明理由.
的取值范围:若不存在,请说明理由.
【答案】(1)证明见解析(2)不存在实数![]() ,详见解析
,详见解析
【解析】
(1)分类讨论,![]() 时直接证明,
时直接证明,![]() 时,利用导数研究函数的单调性,最小值可证得不等式成立;
时,利用导数研究函数的单调性,最小值可证得不等式成立;
(2)![]() 时,由(1)可知无零点,
时,由(1)可知无零点,![]() 时,仍然利用导数研究函数的单调性,函数极值,结合零点存在定理确定零点个数.
时,仍然利用导数研究函数的单调性,函数极值,结合零点存在定理确定零点个数.
(1)证明:①若![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ;
;
②若![]() ,因为
,因为![]() ,
,
设![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
综上所述,若![]() ,
,![]() ,则
,则![]() .
.
(2)不存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上有两个零点.
上有两个零点.
理由如下:
(1)若![]() ,由(1)知,
,由(1)知,![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上无零点;
上无零点;
(2)若![]() ,由(1)知,当
,由(1)知,当![]() 时,
时,![]()
所以![]() 在
在![]() 上单调递增.因为
上单调递增.因为![]() ,
,![]() ,
,
所以![]() 在
在![]() 上存在唯一的零点
上存在唯一的零点![]() ,
,
即方程![]() 在
在![]() 上存在唯一解
上存在唯一解![]() ,
,
且当![]() 时,
时,![]() ,当
,当![]() ,
,![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 无零点;
无零点;
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有唯一零点,
上有唯一零点,
故当![]() 时,
时,![]() 在
在![]() 上有一个零点,
上有一个零点,
综上所述,不存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上有两个零点.
上有两个零点.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 经过点
经过点![]() ,且与极轴所成的角为
,且与极轴所成的角为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】最近几年汽车金融公司发展迅猛,主要受益于监管层面对消费进人门槛的降低,互联网信贷消费的推广普及,以及汽车销售市场规模的扩张.如图是2013﹣2017年汽车金融行业资产规模统计图(单位:亿元).
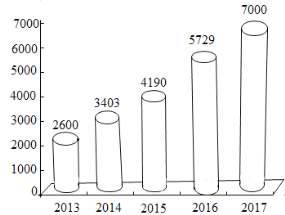
(1)以年份值2013,2014,…为横坐标,汽车金融行业资产规模(单位:亿元)为纵坐标,求y关于x的线性回归方程;
(2)利用(1)中的回归方程,预计2018年汽车金融行业资产规模(精确到亿元).
附:回归直线的斜率和截距的最小二乘估计公式分别为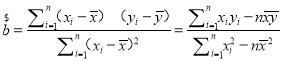 ,
,![]() (其中
(其中![]() ,
,![]() 为样本平均值).
为样本平均值).
参考数据:![]() 4.620×107,2015
4.620×107,2015![]() 4.619×107.
4.619×107.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)令![]() ,已知函数
,已知函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,
,
①求实数![]() 的取值范围;
的取值范围;
②若存在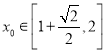 ,使不等式
,使不等式![]() 对任意
对任意![]() (取值范围内的值)恒成立,求实数
(取值范围内的值)恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
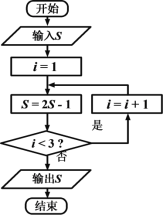
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购已经成为一种新型的购物方式,2018年天猫双11,仅1小时47分钟成交额超过1000亿元,比2017年达到1000亿元的时间缩短了7个小时,为了研究市民对网购的依赖性,从A城市16﹣59岁人群中抽取一个容量为100的样本,得出下列2×2列联表,其中16﹣39岁为青年,40﹣59岁为中年,当日消费金额超过1000元为消费依赖网购,否则为消费不依赖网购.
依赖网购 | 不依赖网购 | 小计 | |
青年(16﹣39岁) | 40 | 20 | |
中年(40﹣59岁) | 20 | 20 | |
小计 |
(1)完成2×2列联表,计算X2值,并判断是否有95%的把握认为网购依赖和年龄有关?
(2)把样本中的频率当作概率,随机从A城市中选取5人,其中依赖网购的人数为随机变量X,求随机变量X的分布列及期望(附:X2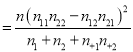 ,当X2>3.841时,有95%的把握说事件A与B有关,当X2≤3.841时,没有95%的把握说事件A与B有关)
,当X2>3.841时,有95%的把握说事件A与B有关,当X2≤3.841时,没有95%的把握说事件A与B有关)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业要设计制造一批大小、规格相同的长方体封闭水箱,已知每个水箱的表面积为432(每个水箱的进出口所占面积与制作材料的厚度均忽略不计).每个长方体水箱的底面长是宽的2倍.现设每个长方体水箱的底面宽是![]() ,用
,用![]() 表示每个长方体水箱的容积.
表示每个长方体水箱的容积.
(1)试求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)当![]() 为何值时,
为何值时,![]() 有最大值,并求出最大值.
有最大值,并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com