
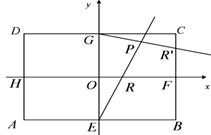
在矩形ABCD中,|AB|=2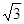 ,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且
,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且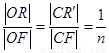 .
.
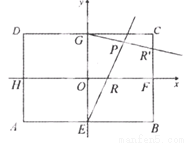
(Ⅰ)求证:直线ER与GR′的交点P在椭圆 :
: +
+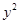 =1上;
=1上;
(Ⅱ)若M、N为椭圆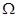 上的两点,且直线GM与直线GN的斜率之积为
上的两点,且直线GM与直线GN的斜率之积为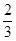 ,求证:直线MN过定点;并求△GMN面积的最大值.
,求证:直线MN过定点;并求△GMN面积的最大值.
 详见解析;
详见解析; 直线MN过定点(0,-3),△GMN面积的最大值
直线MN过定点(0,-3),△GMN面积的最大值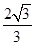 .
.
【解析】
试题分析: 先计算出E、R、G、R′各点坐标,得出直线ER与GR′的方程,解得其交点坐标
先计算出E、R、G、R′各点坐标,得出直线ER与GR′的方程,解得其交点坐标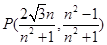 代入满足椭圆方程即可;
代入满足椭圆方程即可;  先讨论直线MN的斜率不存在时的情况;再讨论斜率存在时,用斜截式设出直线MN方程.与椭圆方程联立,用“设而不求”的方法通过韦达定理得出b为定值-3或1,又当b=1时,直线GM与直线GN的斜率之积为0,所以舍去.从而证明出MN过定点(0,-3).最后算出点
先讨论直线MN的斜率不存在时的情况;再讨论斜率存在时,用斜截式设出直线MN方程.与椭圆方程联立,用“设而不求”的方法通过韦达定理得出b为定值-3或1,又当b=1时,直线GM与直线GN的斜率之积为0,所以舍去.从而证明出MN过定点(0,-3).最后算出点 到直线
到直线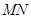 的距离及MN的距离,得出△GMN面积是一个关于
的距离及MN的距离,得出△GMN面积是一个关于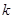 的代数式,由
的代数式,由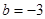 及
及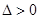 知:
知: ,用换元法利用基本不等式求出△GMN面积的最大值是
,用换元法利用基本不等式求出△GMN面积的最大值是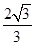 .
.
试题解析:(Ⅰ)∵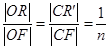 ,∴
,∴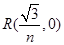 ,
,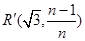 1分
1分
又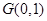 则直线
则直线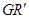 的方程为
的方程为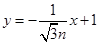 ① 2分
① 2分
又 则直线
则直线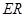 的方程为
的方程为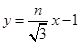 ②
②
由①②得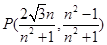
∵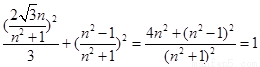
∴直线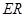 与
与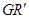 的交点
的交点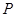 在椭圆
在椭圆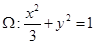 上
4分
上
4分
(Ⅱ)①当直线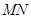 的斜率不存在时,设
的斜率不存在时,设
不妨取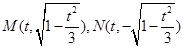 ∴
∴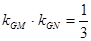 ,不合题意
5分
,不合题意
5分
②当直线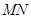 的斜率存在时,设
的斜率存在时,设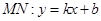
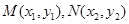

联立方程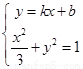 得
得
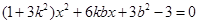
则
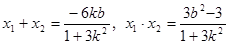 7分
7分
又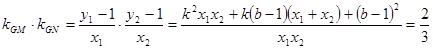
即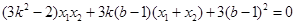
将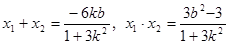 代入上式得
代入上式得
解得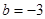 或
或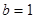 (舍)
(舍)
∴直线过定点 10分
10分
∴ ,点
,点 到直线
到直线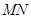 的距离为
的距离为
∴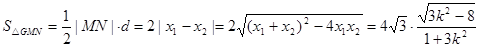
由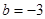 及
及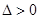 知:
知: ,令
,令 即
即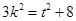
∴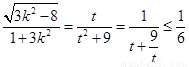 当且仅当
当且仅当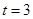 时,
时,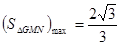 13分
13分
考点:1.直线的方程;2.解析几何;3.基本不等式.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
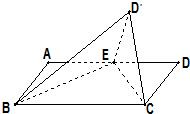 如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.
如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.查看答案和解析>>
科目:高中数学 来源: 题型:
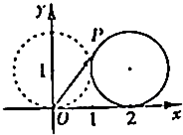 (1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,
(1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,| OP |
|
| ||
|
|
|
| ||
|
|
| AM |
| AN |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com