
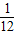 ,用1减去对立事件的概率,即得所求.
,用1减去对立事件的概率,即得所求.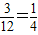 …(6分)
…(6分)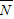 表示“A2,B2全被选 中”这一事件.
表示“A2,B2全被选 中”这一事件.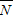 中只有(A2,B2)一种结果.
中只有(A2,B2)一种结果.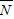 )=
)=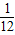 由对立事件的概率公式得:
由对立事件的概率公式得: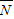 )=1一
)=1一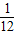 =
=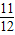 .…(12分)
.…(12分)

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年山东省高一下学期期末考试数学卷 题型:解答题
(本小题满分10分)
某校有学生会干部7名,其中男干部有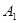 ,A
,A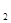 ,A
,A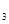 ,A
,A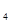 共4人;女干部有B
共4人;女干部有B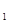 ,B
,B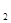 ,B
,B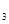 共3人.从中选出男、女干部各1名,组成一个小组参加某项活动.
共3人.从中选出男、女干部各1名,组成一个小组参加某项活动.
(Ⅰ)求A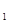 被选中的概率;
被选中的概率;
(Ⅱ)求A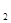 ,B
,B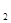 不全被选中的概率.
不全被选中的概率.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
某校有学生会干部7名,其中男干部有![]() ,A
,A![]() ,A
,A![]() ,A
,A![]() 共4人;女干部有B
共4人;女干部有B![]() ,B
,B![]() ,B
,B![]() 共3人.从中选出男、女干部各1名,组成一个小组参加某项活动.
共3人.从中选出男、女干部各1名,组成一个小组参加某项活动.
(Ⅰ)求A![]() 被选中的概率;
被选中的概率;
(Ⅱ)求A![]() ,B
,B![]() 不全被选中的概率.
不全被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com