
【题目】为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生产线的技术改造前后各20次连续正常运行的时间长度(单位:天)数据,并绘制了如下茎叶图:
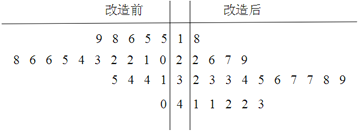
(Ⅰ)(1)设所采集的40个连续正常运行时间的中位数![]() ,并将连续正常运行时间超过
,并将连续正常运行时间超过![]() 和不超过
和不超过![]() 的次数填入下面的列联表:
的次数填入下面的列联表:
超过 | 不超过 | |
改造前 |
|
|
改造后 |
|
|
试写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)根据(1)中的列联表,能否有![]() 的把握认为生产线技术改造前后的连续正常运行时间有差异?
的把握认为生产线技术改造前后的连续正常运行时间有差异?
附: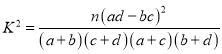 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)工厂的生产线的运行需要进行维护.工厂对生产线的生产维护费用包括正常维护费、保障维护费两种对生产线设定维护周期为![]() 天(即从开工运行到第
天(即从开工运行到第![]() 天(
天(![]() )进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元
)进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元![]() 次;保障维护费第一次为0.2万元
次;保障维护费第一次为0.2万元![]() 周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:
周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:![]() ,
,![]() ,2,3,4.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
,2,3,4.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
【答案】(Ⅰ)(1)![]() ,
,![]() ,
,![]() ,
,![]() ,(2)有
,(2)有![]() 的把握认为连续正常运行时间有差异;(Ⅱ)分布列见解析,2.275万元.
的把握认为连续正常运行时间有差异;(Ⅱ)分布列见解析,2.275万元.
【解析】
(Ⅰ)根据茎叶图得到![]() ,
,![]() ,
,![]() ,
,![]() ,计算
,计算![]() ,得到答案.
,得到答案.
(Ⅱ)计算得到![]() ,得到分布列,计算数学期望得到答案.
,得到分布列,计算数学期望得到答案.
(Ⅰ)(1)由茎叶图知![]() ,根据茎叶图可得:
,根据茎叶图可得:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)由于![]() ,所以有
,所以有![]() 的把握认为连续正常运行时间有差异.
的把握认为连续正常运行时间有差异.
(Ⅱ)生产周期内有4个维护周期,一个维护周期为30天,一个维护周期内,生产线需保障维护的概率为![]() .
.
设一个生产周期内需保障维护的次数为![]() 次,则正常维护费为
次,则正常维护费为![]() 万元,保障维护费为
万元,保障维护费为![]() 万元.
万元.
故一个生产周期内需保障维护![]() 次时的生产维护费为
次时的生产维护费为![]() 万元.
万元.
由于![]() ,设一个生产周期内的生产维护费为
,设一个生产周期内的生产维护费为![]() 万元,则分布列为
万元,则分布列为
| 2 | 2.2 | 2.6 | 3.2 | 4 |
|
|
|
|
|
|
则![]()
![]() 万元.
万元.
故一个生产周期内生产维护费的期望值为2.275万元.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】2019年第十三届女排世界杯共12支参赛球队,比赛赛制釆取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以3—0或3—1取胜的球队积3分,负队积0分;而在比赛中以3—2取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为![]() .
.
(1)第10轮比赛中,记中国队3—1取胜的概率为![]() ,求
,求![]() 的最大值点
的最大值点![]() .
.
(2)以(1)中的![]() 作为
作为![]() 的值.
的值.
(i)在第10轮比赛中,中国队所得积分为![]() ,求
,求![]() 的分布列;
的分布列;
(ⅱ)已知第10轮美国队积3分,判断中国队能否提前一轮夺得冠军(第10轮过后,无论最后一轮即第11轮结果如何,中国队积分最多)?若能,求出相应的概率;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() ,
,![]() 分别是曲线
分别是曲线![]() ,
,![]() 上两动点且
上两动点且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和所支出的维修费用 y(万元),有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料可知y对x呈线性相关关系,且线性回归方程为y=a+bx,其中已知b=1.23,请估计使用年限为20年时,维修费用约为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 是曲线
是曲线![]() (
(![]() 为参数)上的动点,将
为参数)上的动点,将![]() 绕点
绕点![]() 顺时针旋转90°得到
顺时针旋转90°得到![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,直线![]() 与曲线
与曲线![]() 分别相交于异于极点
分别相交于异于极点![]() 的
的![]() 两点,点
两点,点![]() ,当
,当![]() 时,求直线
时,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是
是![]() 上的奇函数,其中
上的奇函数,其中![]() ,则下 列关于函数
,则下 列关于函数![]() 的描述中,其中正确的是( )
的描述中,其中正确的是( )
①将函数![]() 的图象向右平移
的图象向右平移![]() 个单位可以得到函数
个单位可以得到函数![]() 的图象;
的图象;
②函数![]() 图象的一条对称轴方程为
图象的一条对称轴方程为![]() ;
;
③当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ;
;
④函数![]() 在
在![]() 上单调递增.
上单调递增.
A.①③B.③④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() .
.
(1)曲线![]() :
:![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 上异于
上异于![]() ,
,![]() 的点,若直线
的点,若直线![]() 的斜率为1,求直线
的斜率为1,求直线![]() 的斜率;
的斜率;
(2)若![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,直线
,直线![]() :
:![]() .过
.过![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() (
(![]() 在第一象限)两点,与
在第一象限)两点,与![]() 相交于
相交于![]() ,是否存在
,是否存在![]() 使
使![]() 的面积等于
的面积等于![]() 的面积与
的面积与![]() 的面积之和.若存在,求直线
的面积之和.若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com