练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在平面直角坐标系中,一种线性变换对应的2×2矩阵为.

    (1)求点A(,3)在该变换作用下的象.

    (2)求圆x2+y2=1在该变换作用下的新曲线的方程.

     

    (1) (,) (2) x2+4y2=1

    【解析】(1)=,即点A在该变换作用下的象为(,).

    (2)设(x,y)为x2+y2=1上任意一点,在该变换作用下对应的点为(x',y'),有=得有x'2+(2y')2=1,得x'2+4y'2=1,即所求曲线方程为x2+4y2=1.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷（解析版） 题型：选择题

    记Sn是等差数列{an}前n项的和,Tn是等比数列{bn}前n项的积,设等差数列{an}公差d≠0,若对小于2011的正整数n,都有Sn=S2011-n成立,则推导出a1006=0.设等比数列{bn}的公比q≠1,若对于小于23的正整数n,都有Tn=T23-n成立,则(　　)

    (A)b11=1 (B)b12=1 (C)b13=1 (D)b14=1

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷（解析版） 题型：解答题

    已知数列{an}是等差数列,且a2=-1,a5=5.

    (1)求{an}的通项an.

    (2)求{an}前n项和Sn的最小值.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十第十章第七节练习卷（解析版） 题型：填空题

    某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续正确回答出两个问题,即停止答题,晋级下一轮.假设某选手正确回答每个问题的概率都是0.8,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一轮的概率等于　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十第十章第七节练习卷（解析版） 题型：选择题

    10张奖券中有3张是有奖的,某人从中不放回地依次抽两张,则在第一次抽到中奖券的条件下,第二次也抽到中奖券的概率为(　　)

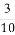    (A) (B) (C) (D)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十四选修4-2第一节练习卷（解析版） 题型：解答题

    2×2矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).

    (1)求矩阵M.

    (2)设直线l在矩阵M对应的变换作用下得到了直线m:x-y=4.求直线l的方程.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十六选修4-2第三节练习卷（解析版） 题型：解答题

    已知矩阵A=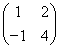,向量α=.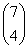

    (1)求A的特征值λ1,λ2和对应的特征向量α1,α2.

    (2)计算A5α的值.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十五选修4-2第二节练习卷（解析版） 题型：解答题

    若曲线C:x2+4xy+2y2=1在矩阵M=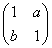对应的线性变换作用下变成曲线C':x2-2y2=1.

    (1)求a,b的值.

    (2)求M的逆矩阵M-1.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷（解析版） 题型：选择题

    关于线性回归,以下说法错误的是(　　)

    (A)自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系

    (B)在平面直角坐标系中用描点的方法得到的表示具有相关关系的两个变量的一组数据的图形叫做散点图

    (C)线性回归直线方程最能代表观测值x,y之间的关系,且其回归直线一定过样本中心点(,)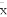

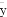    (D)甲、乙、丙、丁四位同学各自对A,B两变量的线性相关性作试验,并由回归分析法分别求得相关系数rxy如下表

     

    甲

    乙

    丙

    丁

    rxy

    0.82

    0.78

    0.69

    0.85

    则甲同学的试验结果体现A,B两变量更强的线性相关性

     

    查看答案和解析>>

    同步练习册答案