
2×2矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(1)求矩阵M.
(2)设直线l在矩阵M对应的变换作用下得到了直线m:x-y=4.求直线l的方程.
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:解答题
已知数列{an}的首项为a1=1,其前n项和为Sn,且对任意正整数n有n,an,Sn成等差数列.
(1)求证:数列{Sn+n+2}成等比数列.
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:填空题
若Sn是等差数列{an}的前n项和,且S8-S3=10,则S11的值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十第十章第七节练习卷(解析版) 题型:选择题
将一枚硬币连掷5次,如果出现k次正面向上的概率等于出现k+1次正面向上的概率,那么k的值为( )
(A)0 (B)1 (C)2 (D)3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十四选修4-2第一节练习卷(解析版) 题型:解答题
在平面直角坐标系中,一种线性变换对应的2×2矩阵为 .
.
(1)求点A( ,3)在该变换作用下的象.
,3)在该变换作用下的象.
(2)求圆x2+y2=1在该变换作用下的新曲线的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,曲线C1的参数方程为 (φ为参数),曲线C2的参数方程为
(φ为参数),曲线C2的参数方程为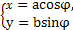 (a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=
(a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=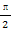 时,这两个交点重合.
时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值.
(2)设当α= 时,l与C1,C2的交点分别为A1,B1,当α=-
时,l与C1,C2的交点分别为A1,B1,当α=- 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十七选修4-4第一节练习卷(解析版) 题型:解答题
在极坐标系下,已知圆O:ρ=cosθ+sinθ和直线l:ρsin(θ- )=
)= .
.
(1)求圆O和直线l的直角坐标方程.
(2)当θ∈(0,π)时,求直线l与圆O公共点的一个极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com