
已知数列{an}的首项为a1=1,其前n项和为Sn,且对任意正整数n有n,an,Sn成等差数列.
(1)求证:数列{Sn+n+2}成等比数列.
(2)求数列{an}的通项公式.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十六第六章第二节练习卷(解析版) 题型:选择题
已知函数y=f(x)的图象如图,则不等式f(3x-x2)<0的解集为( )

(A){x|1<x<2} (B){x|0<x<3}
(C){x|x<1或x>2} (D){x|x<0或x>3}
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十二第五章第三节练习卷(解析版) 题型:解答题
已知数列{an}中,a1=1,前n项和为Sn且Sn+1= Sn+1,n∈N*.
Sn+1,n∈N*.
(1)求数列{an}的通项公式.
(2)求数列{ }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:填空题
已知P(x0,y0)是抛物线y2=2px(p>0)上的一点,过P点的切线方程的斜率可通过如下方式求得:
在y2=2px两边同时求导,得:
2yy'=2p,则y'=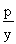 ,所以过P的切线的斜率:k=
,所以过P的切线的斜率:k=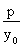 .
.
试用上述方法求出双曲线x2-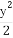 =1在P(
=1在P(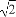 ,
,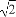 )处的切线方程为 .
)处的切线方程为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:选择题
记Sn是等差数列{an}前n项的和,Tn是等比数列{bn}前n项的积,设等差数列{an}公差d≠0,若对小于2011的正整数n,都有Sn=S2011-n成立,则推导出a1006=0.设等比数列{bn}的公比q≠1,若对于小于23的正整数n,都有Tn=T23-n成立,则( )
(A)b11=1 (B)b12=1 (C)b13=1 (D)b14=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:填空题
已知数列{an}中,a1=1,a2=2,当整数n>1时,Sn+1+Sn-1=2(Sn+S1)都成立,则S5= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:选择题
已知数列{an}的通项公式是an=2n-3( )n,则其前20项和为( )
)n,则其前20项和为( )
(A)380- (1-
(1-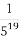 )(B)400-
)(B)400- (1-
(1-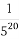 )
)
(C)420- (1-
(1-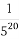 )(D)440-
)(D)440- (1-
(1-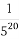 )
)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:选择题
若不等式Ax+By+5<0表示的平面区域不包括点(2,4),且k=A+2B,则k的取值范围是( )
(A)k≥- (B)k≤-
(B)k≤-
(C)k>- (D)k<-
(D)k<-
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十四选修4-2第一节练习卷(解析版) 题型:解答题
2×2矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(1)求矩阵M.
(2)设直线l在矩阵M对应的变换作用下得到了直线m:x-y=4.求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com