
在极坐标系下,已知圆O:ρ=cosθ+sinθ和直线l:ρsin(θ- )=
)= .
.
(1)求圆O和直线l的直角坐标方程.
(2)当θ∈(0,π)时,求直线l与圆O公共点的一个极坐标.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十四选修4-2第一节练习卷(解析版) 题型:解答题
2×2矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(1)求矩阵M.
(2)设直线l在矩阵M对应的变换作用下得到了直线m:x-y=4.求直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:填空题
若随机变量ξ的分布列为:P(ξ=m)= ,P(ξ=n)=a.若E(ξ)=2,则D(ξ)的最小值等于 .
,P(ξ=n)=a.若E(ξ)=2,则D(ξ)的最小值等于 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:选择题
通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的2×2列联表:
| 男 | 女 | 总计 |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由χ2= 算得,
算得,
χ2= ≈7.8.
≈7.8.
以下结论正确的是( )
(A)有99%以上的把握认为“选择过马路的方式与性别有关”
(B)有99%以上的把握认为“选择过马路的方式与性别无关”
(C)在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
(D)在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:选择题
关于线性回归,以下说法错误的是( )
(A)自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
(B)在平面直角坐标系中用描点的方法得到的表示具有相关关系的两个变量的一组数据的图形叫做散点图
(C)线性回归直线方程最能代表观测值x,y之间的关系,且其回归直线一定过样本中心点(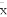 ,
,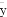 )
)
(D)甲、乙、丙、丁四位同学各自对A,B两变量的线性相关性作试验,并由回归分析法分别求得相关系数rxy如下表
| 甲 | 乙 | 丙 | 丁 |
rxy | 0.82 | 0.78 | 0.69 | 0.85 |
则甲同学的试验结果体现A,B两变量更强的线性相关性
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:填空题
随机变量η的分布列如下:
η | 1 | 2 | 3 | 4 | 5 | 6 |
P | 0.2 | x | 0.35 | 0.1 | 0.15 | 0.2 |
则①x= ;②P(η>3)= ;
③P(1<η≤4)= .
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数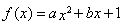 在
在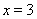 处的切线方程为
处的切线方程为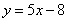 .
.
(1)求函数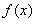 的解析式;
的解析式;
(2)若关于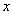 的方程
的方程 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数 的值;
的值;
(3)数列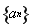 满足
满足 ,
,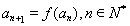 ,求
,求 的整数部分.
的整数部分.
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:填空题
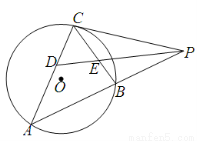
如图,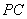 是圆
是圆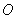 的切线,切点为点
的切线,切点为点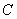 ,直线
,直线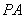 与圆
与圆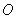 交于
交于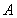 、
、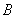 两点,
两点,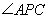 的角平分线交弦
的角平分线交弦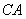 、
、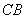 于
于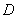 、
、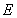 两点,已知
两点,已知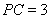 ,
,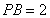 ,则
,则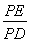 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com