
(本小题满分10分)选修4-5:不等式选讲
设函数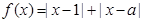 .
.
(Ⅰ)若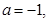 解不等式
解不等式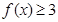 ;
;
(Ⅱ)如果关于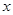 的不等式
的不等式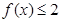 有解,求
有解,求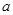 的取值范围.
的取值范围.
(Ⅰ)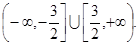 (Ⅱ)
(Ⅱ)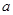 的取值范围为
的取值范围为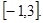
【解析】本试题主要是考查了绝对值不等式的求解,以及关系与参数的取值范围的问题的综合运用。
(1)因为当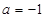 时,
时,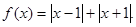
由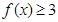 ,得,
,得,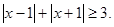
然后分为三段论求解得到解集。
(2)因为关于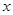 的不等式
的不等式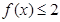 有解,所以,
有解,所以,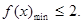 ,进而得到参数的范围。
,进而得到参数的范围。
(Ⅰ)当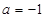 时,
时,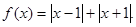
由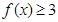 ,得,
,得,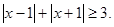
① 当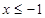 时,不等式化为
时,不等式化为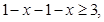 即
即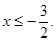
所以,原不等式的解为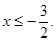 ----------------1分
----------------1分
② 当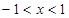 时,不等式化为
时,不等式化为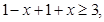 即
即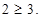
所以,原不等式无解. ----------------2分
③ 当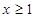 时,不等式化为
时,不等式化为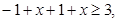 即
即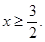
所以,原不等式的解为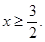 ----------------3分
----------------3分
综上,原不等式的解为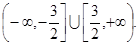 ----------------4分
----------------4分
(说明:若考生按其它解法解答正确,相应给分)
(Ⅱ)因为关于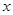 的不等式
的不等式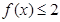 有解,所以,
有解,所以,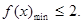 ----------------5分
----------------5分
因为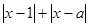 表示数轴上的点到
表示数轴上的点到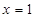 与
与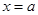 两点的距离之和,
两点的距离之和,
所以,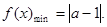 ----------------6分
----------------6分
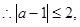
解得,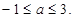
所以,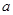 的取值范围为
的取值范围为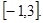 ----------------7分
----------------7分


科目:高中数学 来源: 题型:
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com