
【题目】已知点G是△ABC的重心,且AG⊥BG, ![]() +
+ ![]() =
= ![]() ,则实数λ的值为( )
,则实数λ的值为( )
A.![]()
B.![]()
C.3
D.2
【答案】B
【解析】解:如图,连接CG,延长交AB于D,
由于G为重心,故D为中点,
∵AG⊥BG,∴DG= ![]() AB,
AB,
由重心的性质得,CD=3DG,即CD= ![]() AB,
AB,
由余弦定理得,AC2=AD2+CD2﹣2ADCDcos∠ADC,
BC2=BD2+CD2﹣2BDCDcos∠BDC,
∵∠ADC+∠BDC=π,AD=BD,
∴AC2+BC2=2AD2+2CD2 ,
∴AC2+BC2= ![]() AB2+
AB2+ ![]() AB2=5AB2 ,
AB2=5AB2 ,
又∵ ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() ,即λ=
,即λ= ![]() ,
,
∴λ= ![]() =
= ![]()
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
即 ![]() .
.
故选B.
【考点精析】关于本题考查的同角三角函数基本关系的运用和正弦定理的定义,需要了解同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() ;正弦定理:
;正弦定理:![]() 才能得出正确答案.
才能得出正确答案.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加数学文化知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:

(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加正式比赛,从所抽取的两组数据求出甲、乙两位同学的平均值和方差,据此你认为选派哪位同学参加比赛较为合适?
(Ⅲ)若对加同学的正式比赛成绩进行预测,求比赛成绩高于80分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,Sn为数列{an}的前n项和,a1=b1=1,且b3S3=36,b2S2=8(n∈N*).
(1)求数列{an}和{bn}的通项公式;
(2)若an<an+1 , 求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
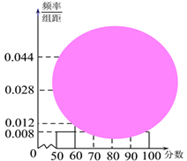
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图:
![]() 求分数在
求分数在![]() 的频率及全班人数;
的频率及全班人数;
![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为C的圆:(x﹣a)2+(y﹣b)2=8(a,b为正整数)过点A(0,1),且与直线y﹣3﹣2 ![]() =0相切.
=0相切.
(1)求圆C的方程;
(2)若过点M(4,﹣1)的直线l与圆C相交于E,F两点,且 ![]() =0.求直线l的方程.
=0.求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对函数 ![]() ,有下列说法:
,有下列说法:
①f(x)的周期为4π,值域为[﹣3,1];
②f(x)的图象关于直线 ![]() 对称;
对称;
③f(x)的图象关于点 ![]() 对称;
对称;
④f(x)在 ![]() 上单调递增;
上单调递增;
⑤将f(x)的图象向左平移 ![]() 个单位,即得到函数
个单位,即得到函数 ![]() 的图象.
的图象.
其中正确的是 . (填上所有正确说法的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
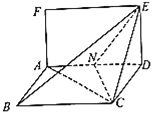
【题目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如图,其中
所在平面互相垂直,如图,其中![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ)试问在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?若存在,请证明
?若存在,请证明![]() 平面
平面![]() ,并求出
,并求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
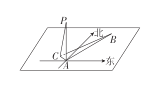
【题目】在海岛![]() 上有一座海拔
上有一座海拔![]() 的山峰,山顶设有一个观察站
的山峰,山顶设有一个观察站![]() ,有一艘轮船按一固定方向做匀速直线航行,上午
,有一艘轮船按一固定方向做匀速直线航行,上午![]() 时,测得此船在岛北偏东
时,测得此船在岛北偏东![]() 、俯角为
、俯角为![]() 的
的![]() 处,到
处,到![]() 时,又测得该船在岛北偏西
时,又测得该船在岛北偏西![]() 、俯角
、俯角![]() 为的
为的![]() 处.
处.
(1)求船的航行速度;
(2)求船从![]() 到
到![]() 行驶过程中与观察站
行驶过程中与观察站![]() 的最短距离.
的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)对于任意实数x,不等式sin x+cos x>m恒成立,求实数m的取值范围;
(2)存在实数x,不等式sin x+cos x>m有解,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com