Question

【题目】已知数列{an}的前n项和Sn=an+n2﹣1，数列{bn}满足3nbn+1=（n+1）an+1﹣nan ， 且b1=3，a1=3．
（1）求数列{ an}和{bn}的通项an ， bn；
（2）设Tn为数列{bn}的前n项和，求Tn ， 并求满足Tn＜7时n的最大值．

Answer 1

【答案】
（1）解：∵Sn=an+n2﹣1，

∴当n≥2时，an=Sn﹣Sn﹣1=（an+n2﹣1）﹣[an﹣1+（n﹣1）2﹣1]，化为：an﹣1=2n﹣1，

又∵a1=1+2=3满足上式，

∴an=2n+1，

∵3nbn+1=（n+1）an+1﹣nan，

∴bn+1= [（n+1）an+1﹣nan]= [（n+1）（2n+3）﹣n（2n+1）]=（4n+3） ，

又∵b1=3满足上式，

∴bn=（4n﹣1） ．

（2）解：由（1）可知，Tn=31+7 +11 +…+（4n﹣1） ，

Tn=3 +7 +…+（4n﹣5） +（4n﹣1） ，

错位相减得： Tn=3+4（ + +…+ ）﹣（4n﹣1） ，

∴Tn= [3+4× 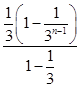﹣（4n﹣1） ]

= ﹣ ，

Tn﹣Tn+1= ﹣ ﹣ = ＜0．

∴Tn＜Tn+1，即{Tn}为递增数列．

又T3= ＜7，T4= ＞7，

∴Tn＜7时，n的最大值为3．

【解析】（1）Sn=an+n2﹣1，当n≥2时，an=Sn﹣Sn﹣1，n=1时满足上式，可得an=2n+1.3nbn+1=（n+1）an+1﹣nan，可得bn+1= [（n+1）an+1﹣nan]=（4n+3） ，又b1=3满足上式，可得bn=（4n﹣1） ．（2）利用错位相减法与等比数列的求和公式可得Tn．可得Tn﹣Tn+1＜0．即可得出．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系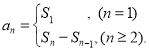；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．