
分析 根据题意,由双曲线的标准方程可得该双曲线的焦点在x轴上,且a=$\sqrt{m}$,b=$\sqrt{6}$,可得其渐近线方程为y=±$\frac{\sqrt{6}}{\sqrt{m}}$x,进而结合题意可得$\frac{\sqrt{6}}{\sqrt{m}}$=1,解可得m的值,即可得答案.
解答 解:根据题意,双曲线的标准方程为:$\frac{x^2}{m}-\frac{y^2}{6}=1$,
则其焦点在x轴上,且a=$\sqrt{m}$,b=$\sqrt{6}$,
故其渐近线方程为y=±$\frac{\sqrt{6}}{\sqrt{m}}$x,
又由该双曲线的一条渐近线方程为y=x,
则有$\frac{\sqrt{6}}{\sqrt{m}}$=1,解可得m=6;
故答案为:6.
点评 本题考查双曲线的简单几何性质,涉及双曲线渐近线的求法,关键是明确双曲线焦点的位置.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
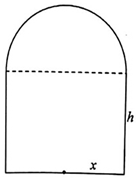 某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,7) | B. | (7,7) | C. | (7,1) | D. | (3,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com