
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 年推销金额y/万元 | 60 | 90 | 90 | 120 | 150 |
分析 (1)根据表中数据,画出散点图即可;
(2)由题意计算平均数与回归系数,写出线性回归方程;
(3)利用回归方程计算x=11时的函数值即可.
解答 解:(1)根据表中数据,画出散点图如下: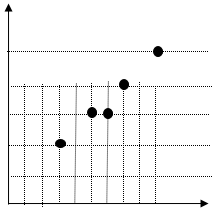
(2)由题意计算得:$\overline x=6,\overline y=10.2,\sum_{i=1}^5{{x_i}{y_i}=336,\sum_{i=1}^5{{x_i}^2}}=200$,
所以$\hat b=\frac{{\sum_{i=1}^5{{x_i}{y_i}-5\bar x\bar y}}}{{\sum_{i=1}^5{{x_i}^2-5{{\bar x}^2}}}}=\frac{334-5×6×10.2}{{200-5×{6^2}}}=1.5$,
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=10.2-1.5×6=1.2;
故年推销金额y关于工作年限x的线性回归方程为$\hat y=1.5x+1.2$;
(3)由(2)知当x=11时,$\hat y=1.5x+1.2=1.5×11+1.2=17.7$,
所以可估计他的年推销金额大约为17.7万元.
点评 本题考查了线性回归方程的求法与应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 110 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | $[\frac{1}{2},2]$ | C. | $[\frac{5}{4},2]$ | D. | $[0,\frac{4}{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{N}{n}$ | B. | n | C. | [$\frac{N}{n}$] | D. | [$\frac{N}{n}$]+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com