已知.(1)当,时,若不等式恒成立,求的范围,(2)试判断函数在内零点的个数.并说明理由. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

已知

.
(1)当

时,若不等式

恒成立,求

的范围；
(2)试判断函数

在

内零点的个数，并说明理由.

（1）

，（2）存在唯一的零点.

试题分析：（1）不等式恒成立问题，通常利用变量分离法转化为求最值问题. 由

, 则

,不等式

恒成立就转化为

，又

在

上是增函数,

，所以

.（2）判断函数

在

内零点的个数，关键分析其在

图像走势，即单调性变化情况. 因为

是增函数, 所以

在

内至多存在一个的零点.又

，

由零点存在性定理有

在

内至少存在一个的零点.两者综合得：

在

内存在唯一的零点.
[解] (1)由

, 则

, 2分
又

在

上是增函数,

4分
所以

. 6分
(2)

是增函数,且

， 8分

12分
所以

在

内存在唯一的零点. 14分

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：不详 题型：解答题

（12分）（2011•福建）设函数f（θ）=

，其中，角θ的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P（x，y），且0≤θ≤π．
（Ⅰ）若点P的坐标为

，求f（θ）的值；
（Ⅱ）若点P（x，y）为平面区域Ω：

上的一个动点，试确定角θ的取值范围，并求函数f（θ）的最小值和最大值．

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

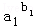
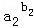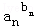（2011•湖北）（1）已知函数f（x）=lnx﹣x+1，x∈（0，+∞），求函数f（x）的最大值；
（2）设a₁，b₁（k=1，2…，n）均为正数，证明：
①若a₁b₁+a₂b₂+…a_nb_n≤b₁+b₂+…b_n，则

…

≤1；
②若b₁+b₂+…b_n=1，则

≤

…

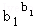
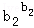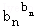≤b₁²+b₂²+…+b_n²．

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

某市居民自来水收费标准如下：每户每月用水不超过4吨时，每吨为1.80元，当用水超过4吨时，超过部分每吨3.00元，某月甲、乙两户共交水费y元，已知甲、乙两户该月用水量分别为5x吨、3x吨．
(1)求y关于x的函数；
(2)若甲、乙两户该月共交水费26.4元，分别求出甲、乙两户该月的用水量和水费．

查看答案和解析>>

科目：高中数学 来源：不详 题型：填空题

具有性质：

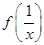＝－f(x)的函数，我们称为满足“倒负”变换的函数，下列函数：
①y＝x－

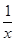；②y＝x＋

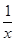；③y＝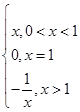

，其中满足“倒负”变换的函数是________(填序号)．

查看答案和解析>>

科目：高中数学 来源：不详 题型：填空题

已知集合M={

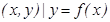}，若对于任意

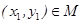，存在

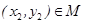，使得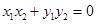

成立，则称集合M是“垂直对点集”．给出下列四个集合：
①M={

}；
②M={

}；
③M={

}；
④M={

}．
其中是“垂直对点集”的序号是；

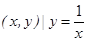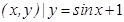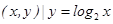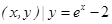查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

某地一渔场的水质受到了污染．渔场的工作人员对水质检测后，决定往水中投放一种药剂来净化水质. 已知每投放质量为

个单位的药剂后，经过x天该药剂在水中释放的浓度y（毫克/升）满足y=mf(x)，其中

，当药剂在水中释放的浓度不低于6（毫克/升）时称为有效净化；当药剂在水中释放的浓度不低于6（毫克/升）且不高于18（毫克/升）时称为最佳净化.
（1）如果投放的药剂质量为m=6，试问渔场的水质达到有效净化一共可持续几天?
（2）如果投放的药剂质量为m，为了使在8天（从投放药剂算起包括第8天）之内的渔场的水质达到最佳净化，试确定应该投放的药剂质量m的取值范围.

查看答案和解析>>

科目：高中数学 来源：不详 题型：单选题

函数y＝

，x∈(－π，0)∪(0，π)的图象可能是下列图象中的(　　)

查看答案和解析>>

科目：高中数学 来源：不详 题型：填空题

函数

的单调递减区间是________________.

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学