
【题目】对于实数![]() 和
和![]() ,定义运算“*”:
,定义运算“*”:![]() ,设
,设![]() ,且关于
,且关于![]() 的方程为
的方程为![]() 恰有三个互不相等的实数根
恰有三个互不相等的实数根![]() ,则
,则![]() 的取值范围是_________.
的取值范围是_________.
科目:高中数学 来源: 题型:
【题目】在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如右面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120 km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )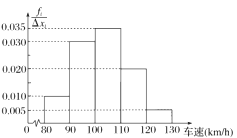
A.30辆
B.1700辆
C.170辆
D.300辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季,甲、乙两名篮球运动员都参加了![]() 场比赛,比赛得分情况如下(单位:分)
场比赛,比赛得分情况如下(单位:分)
甲:![]()
乙:![]()

(1)根据得分情况记录,作出两名篮球运动员得分的茎叶图,并根据茎叶图,对甲、乙两运动员得分作比较,写出两个统计结论;
(2)设甲篮球运动员![]() 场比赛得分平均值
场比赛得分平均值![]() ,将
,将![]() 场比赛得分
场比赛得分![]() 依次输入如图所示的程序框图进行运算,问输出的
依次输入如图所示的程序框图进行运算,问输出的![]() 大小为多少?并说明
大小为多少?并说明![]() 的统计学意义;
的统计学意义;
(3)如果从甲、乙两位运动员的![]() 场得分中,各随机抽取一场不少于
场得分中,各随机抽取一场不少于![]() 分的得分,求甲的得分大于乙的得分的概率.
分的得分,求甲的得分大于乙的得分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某淘宝商城在2017年前7个月的销售额![]() (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知![]() 与
与![]() 具有较好的线性关系.
具有较好的线性关系. 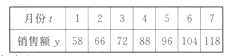
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
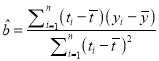 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x2﹣x﹣6≤0}, ![]() ,那么集合A∩(UB)=( )
,那么集合A∩(UB)=( )
A.[﹣2,4)
B.(﹣1,3]
C.[﹣2,﹣1]
D.[﹣1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若对任意的
时,若对任意的![]() ,总存在
,总存在![]() 使
使![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 的值域为区间
的值域为区间![]() ,是否存在常数
,是否存在常数![]() ,使区间
,使区间![]() 的长度为
的长度为![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由.(柱:区间
的值,若不存在,请说明理由.(柱:区间![]() 的长度为
的长度为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]()
(1) 证明:数列![]() 是等比数列;
是等比数列;
(2) 求使不等式![]() 成立的所有正整数m、n的值;
成立的所有正整数m、n的值;
(3) 如果常数0 < t < 3,对于任意的正整数k,都有![]() 成立,求t的取值范围.
成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究下学习中,关于三角形与三角函数知识的应用(约定三内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() )得出如下一些结论:
)得出如下一些结论:
(1)若![]() 是钝角三角形,则
是钝角三角形,则![]() ;
;
(2)若![]() 是锐角三角形,则
是锐角三角形,则![]() ;
;
(3)在三角形![]() 中,若
中,若![]() ,则
,则![]() ;
;
(4)在![]() 中,若
中,若![]() ,
,![]() ,则
,则![]() .其中错误命题的个数是( )
.其中错误命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com