
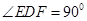 ,
,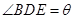 ,
,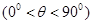 .
.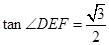 时,求
时,求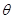 的大小;
的大小;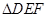 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时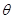 的值.
的值.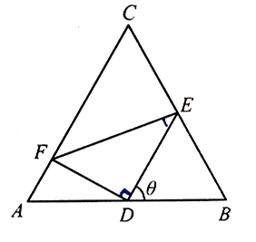
 .
. 中,
中, ,①,而在
,①,而在 中,利用正弦定理,用
中,利用正弦定理,用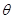 表示DE,在
表示DE,在 中,利用正弦定理,用
中,利用正弦定理,用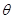 表示DF,代入到①式中,再利用两角和的正弦公式展开,解出
表示DF,代入到①式中,再利用两角和的正弦公式展开,解出 ,利用特殊角的三角函数值求角
,利用特殊角的三角函数值求角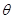 ;第二问,将第一问得到的DF和DE代入到三角形面积公式中,利用两角和的正弦公式和倍角公式化简表达式,利用正弦函数的有界性确定S的最小值.
;第二问,将第一问得到的DF和DE代入到三角形面积公式中,利用两角和的正弦公式和倍角公式化简表达式,利用正弦函数的有界性确定S的最小值.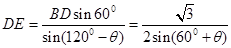 ,
,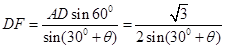 . 4分
. 4分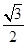 ,得
,得 ,整理得
,整理得 ,
,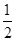 DE·DF=
DE·DF=
 . 10分
. 10分 . 12分
. 12分

科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
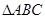 中,
中,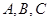 的对边分别为
的对边分别为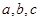 且
且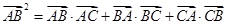 .
.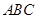 的形状,并求
的形状,并求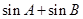 的取值范围;
的取值范围;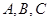 的顶点
的顶点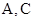 分别在
分别在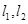 上运动,
上运动,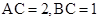 ,若直线
,若直线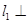 直线
直线 ,且相交于点
,且相交于点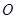 ,求
,求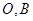 间距离的取值范围.
间距离的取值范围.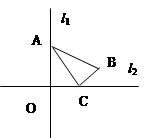
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.b = 10,A = 45°,B = 70° |
| B.a = 60,c = 48,B = 100° |
| C.a = 14,b = 16,A = 45° |
| D.a = 7,b = 5,A = 80° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com