
如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.
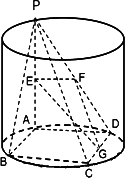
(1)求证:平面PDC⊥平面PAD;
(2)求证:PB//面EFG;
(3)在线段BC上是否存在一点M,使得D到平面PAM的距离为2?若存在,求出BM;若不存在,请说明理由.
|
证明(1)∵PA是圆柱的母线,∴PA ∵CD 又∵ABCD为矩形,∴CD 而AD 又CD (2)取AB中点H,连结GH,HE, ∵E,F,G分别是线段PA、PD、CD的中点, ∴GH∥AD∥EF, ∴E,F,G,H四点共面.6分 又H为AB中点,∴EH∥PB.7分 又 ∴PB∥面EFG.9分 (3)假设在BC上存在一点M,使得点D到平面PAM的距离为2,则以 由(2)知PA ∴VD-PAM= ∵ ∴ ∵VD-PAM= ∴ ∵ ∴在BC上存在一点M,当
|


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图所示,圆柱的高为2,底面半径为
如图所示,圆柱的高为2,底面半径为| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•茂名二模)如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.
(2012•茂名二模)如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•广州三模)如图所示,圆柱的高为2,底面半径为
(2013•广州三模)如图所示,圆柱的高为2,底面半径为| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•韶关一模)如图所示,圆柱的高为2,底面半径为
(2012•韶关一模)如图所示,圆柱的高为2,底面半径为| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
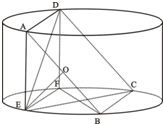 如图所示,圆柱的高为2,底面半径为
如图所示,圆柱的高为2,底面半径为| 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com