练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    观察下面一组组合数等式：
    ；
    ；
    ；
    …………
    （1）由以上规律，请写出第个等式并证明；
    （2）随机变量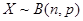，求证：.

    (1) ；（2）详见解析．

    解析试题分析：(1)观察等式规律，易得，有组合数计算公式易证出．（2）随机变量，求证：，显然这是一个二项分布，根据二项分布得，利用(1)的结论，及二项式定理，即可证明．
    试题解析：（1），证略.
    (2)由二项分布得：

    .
    考点：归纳推理，二项分布与数学期望．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    乒乓球比赛规则规定：一局比赛，双方比分在10平前，一方连续发球2次后，对方再连续发球2次，依次轮换.每次发球，胜方得1分，负方得0分.设在甲、乙的比赛中，每次发球，发球方得1分的概率为0.6，各次发球的胜负结果相互独立.甲、乙的一局比赛中，甲先发球.
    （1）求开始第4次发球时，甲、乙的比分为1比2的概率；
    （2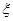）表示开始第4次发球时乙的得分，求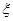的期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    第16届亚运会于2010年11月12日在广州举办，运动会期间来自广州大学和中山大学的共计6名大学生志愿者将被随机平均分配到跳水、篮球、体操这三个比赛场馆服务，且跳水场馆至少有一名广州大学志愿者的概率是.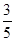
    (1)求6名志愿者中来自广州大学、中山大学的各有几人？
    (2)设随机变量X为在体操比赛场馆服务的广州大学志愿者的人数，求X的分布列及均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    A、B两个投资项目的利润率分别为随机变量X1和X2，根据市场分析，X1和X2的分布列分别为

    X1
    		5%
    		10%
    P
    		0.8
    		0.2
     
    X2
    		2%
    		8%
    		12%
    P
    		0.2
    		0.5
    		0.3
    (1)在A，B两个项目上各投资100万元，Y1和Y2分别表示投资项目A和B所获得的利润，求方差V(Y1)、V(Y2)；
    (2)将x(0≤x≤100)万元投资A项目，100－x万元投资B项目，f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和．求f(x)的最小值，并指出x为何值时，f(x)取到最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设甲、乙、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.三人各向目标射击一次，求至少有一人命中目标的概率及恰有两人命中目标的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某校组织一次冬令营活动，有8名同学参加，其中有5名男同学，3名女同学，为了活动的需要，要从这8名同学中随机抽取3名同学去执行一项特殊任务，记其中有X名男同学．
    (1)求X的分布列；
    (2)求去执行任务的同学中有男有女的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设连续掷两次骰子得到的点数分别为m、n，令平面向量a＝(m，n)，b＝(1，－3)．
    (1) 求使得事件“a⊥b”发生的概率；
    (2) 求使得事件“|a|≤|b|”发生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲、乙、丙三个车床加工的零件分别为350个，700个，1050个，现用分层抽样的方法随机抽取6个零件进行检验.
    （1）从抽取的6个零件中任意取出2个，已知这两个零件都不是甲车床加工的，求其中至少有一个是乙车床加工的零件；
    （2）从抽取的6个零件中任意取出3个，记其中是乙车床加工的件数为X，求X的分布列和期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了倡导健康、低碳、绿色的生活理念，某市建立了公共自行车服务系统鼓励市民租用公共自行车出行，公共自行车按每车每次的租用时间进行收费，具体收费标准如下：
    ①租用时间不超过1小时，免费；
    ②租用时间为1小时以上且不超过2小时，收费1元；
    ③租用时间为2小时以上且不超过3小时，收费2元；
    ④租用时间超过3小时的时段，按每小时2元收费（不足1小时的部分按1小时计算）
    已知甲、乙两人独立出行，各租用公共自行车一次，两人租车时间都不会超过3小时，设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
    （1）求甲、乙两人所付租车费相同的概率；
    （2）设甲、乙两人所付租车费之和为随机变量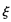，求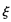的分布列和数学期望E.

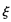    查看答案和解析>>

    同步练习册答案