
为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励市民租用公共自行车出行,公共自行车按每车每次的租用时间进行收费,具体收费标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,收费1元;
③租用时间为2小时以上且不超过3小时,收费2元;
④租用时间超过3小时的时段,按每小时2元收费(不足1小时的部分按1小时计算)
已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
(1)求甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付租车费之和为随机变量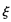 ,求
,求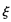 的分布列和数学期望E
的分布列和数学期望E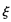 .
.
(1)0.37; (2)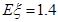
解析试题分析:(1) 由于甲、乙付费的情况有三种,所以每种是相互独立的.又因为甲、乙两人所付租车费相同的概率的含义即把他们各自在三种情况下的概率计算好,然后分别将甲、乙负相同车费的概率分别相乘,然后求和.即可的结论.
(2)因为甲、乙两人所付租车费之和为随机变量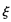 ,共有五种情况,根据题意写出每种
,共有五种情况,根据题意写出每种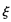 的概率,列出分布列的表,再根据数学期望的计算公式即得到结论.
的概率,列出分布列的表,再根据数学期望的计算公式即得到结论.
试题解析:(1)根据题意,分别记“甲所付租车费0元、1元、2元”为事件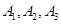 ,它们彼此互斥,
,它们彼此互斥,
且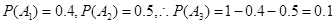
分别记“乙所付租车费0元、1元、2元”为事件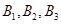 ,它们彼此互斥,
,它们彼此互斥,
且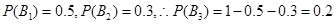
由题知,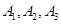 与
与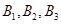 相互独立,
相互独立,
记甲、乙两人所付租车费相同为事件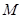 ,则
,则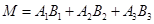
所以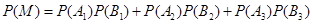
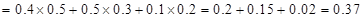
(2) 据题意 的可能取值为:
的可能取值为: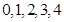

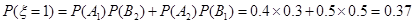
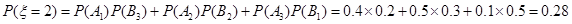

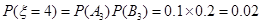
所以 的分布列为:
的分布列为:
0 1 2 3 4 P 0.2 0.37 0.28 0.13 0.02  的数学期望
的数学期望
答:甲、乙两人所扣积分相同的概率为0.37, 的数学期望
的数学期望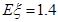
考点:1.概率的含义.2.数学期望的计算方法.3.分类的思想.4.运算能力.


科目:高中数学 来源: 题型:解答题
现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为合格.假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋中装有若干个大小相同的黑球、白球和红球,已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.
(1)若袋中共有10个球,
①求白球的个数;
②从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
(2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于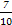 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
中国男子篮球职业联赛总决赛采用七场四胜制(即先胜四场者获胜).进入总决赛的甲乙两队中,若每一场比赛甲队获胜的概率为 ,乙队获胜的概率为
,乙队获胜的概率为 ,假设每场比赛的结果互相独立.现已赛完两场,乙队以
,假设每场比赛的结果互相独立.现已赛完两场,乙队以 暂时领先.
暂时领先.
(1)求甲队获得这次比赛胜利的概率;
(2)设比赛结束时两队比赛的场数为随机变量 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图: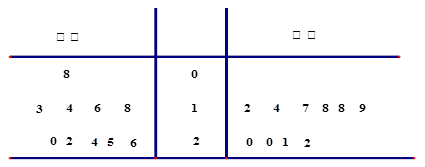
规定:当产品中的此种元素含量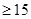 毫克时为优质品.
毫克时为优质品.
(1)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(2)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数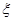 的分布列及数学期望
的分布列及数学期望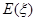 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆.
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
 .记这8辆轿车的得分的平均数为
.记这8辆轿车的得分的平均数为 ,定义事件
,定义事件 {
{ ,且函数
,且函数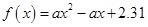 没有零点},求事件
没有零点},求事件 发生的概率.
发生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市准备从7名报名者(其中男4人,女3人)中选3人到三个局任副局长.
(1)设所选3人中女副局长人数为X,求X的分布列和数学期望;
(2)若选派三个副局长依次到A、B、C三个局上任,求A局是男副局长的情况下,B局为女副局长的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com