
【题目】某个体户计划经销A,B两种商品,据调查统计,当投资额为x(x≥0)万元时,在经销A,B商品中所获得的收益分别为f(x)万元与g(x)万元,其中f(x)=a(x-1)+2,g(x)=6ln(x+b)(a>0,b>0).已知投资额为零时收益为零.
(1)求a,b的值;
(2)如果该个体户准备投入5万元经销这两种商品,请你帮他制定一个资金投入方案,使他能获得最大利润.
【答案】(1)a=2,b=1;(2)答案见解析.
【解析】
(1)利用已知条件通过f(0)=0,g(0)=0即可得出a、b的值。
(2)设投入B商品的资金为x万元(0<x≤5) 则投入经销A商品的资金为(5-x)万元,
设所获得的收益为S(x)万元,则S(x)=2(5-x)+6ln (x+1)=6ln (x+1)-2x+10,(0<x≤5)通过函数的导数,求出函数的最值即可。
(1)由投资额为零时收益为零,
可知f(0)=-a+2=0,g(0)=6ln b=0,
解得a=2,b=1.
(2)由(1)可得f(x)=2x,g(x)=6ln (x+1).
设投入经销B商品的资金为x万元(0<x≤5),
则投入经销A商品的资金为(5-x)万元,
设所获得的收益为S(x)万元,则S(x)=2(5-x)+6ln (x+1)=6ln (x+1)-2x+10(0<x≤5).
S′(x)=![]() -2,令S′(x)=0,得x=2.
-2,令S′(x)=0,得x=2.
当0<x<2时,S′(x)>0,函数S(x)单调递增;
当2<x≤5时,S′(x)<0,函数S(x)单调递减.
所以,当x=2时,函数S(x)取得最大值,S(x)max=S(2)=6ln 3+6≈12.6万元.
所以,当投入经销A商品3万元,B商品2万元时,他可获得最大收益,收益的最大值约为12.6万元.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得![]() =80,
=80, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,  ,a=
,a=![]() -b
-b![]() ,其中
,其中![]() ,
, ![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
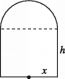
【题目】某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
(1)写出S关于x的函数关系式;
(2)如何设计瓶子的尺寸(不考虑瓶壁的厚度),可以使表面积S最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1+cosωx,1),
=(1+cosωx,1), ![]() =(1,a+
=(1,a+ ![]() sinωx)(ω为常数且ω>0),函数f(x)=
sinωx)(ω为常数且ω>0),函数f(x)= ![]() 在R上的最大值为2.
在R上的最大值为2.
(1)求实数a的值;
(2)把函数y=f(x)的图象向右平移 ![]() 个单位,可得函数y=g(x)的图象,若y=g(x)在[0,
个单位,可得函数y=g(x)的图象,若y=g(x)在[0, ![]() ]上为增函数,求ω的最大值.
]上为增函数,求ω的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在8件获奖作品中,有3件一等奖,有5件二等奖,从这8件作品中任取3件.
(1)求取出的3件作品中,一等奖多于二等奖的概率;
(2)设X为取出的3件作品中一等奖的件数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某旅游城市在过去的一个月内(以30天计),第t天(1≤t≤30,t∈N*)的旅游人数f(t)(单位:万人)近似地满足f(t)=4+ ![]() ,而人均日消费俄g(t)(单位:元)近似地满足g(t)=
,而人均日消费俄g(t)(单位:元)近似地满足g(t)= ![]() .
.
(1)试求所有游客在该城市旅游的日消费总额W(t)(单位:万元)与时间t(1≤t≤30,t∈N*)的函数表达式;
(2)求所有游客在该城市旅游的日消费总额的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com