
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1 , E、F分别是CC1 , BC的中点. 
(1)求证:平面AB1F⊥平面AEF;
(2)求二面角B1﹣AE﹣F的余弦值.
【答案】
(1)证明:连结AF,∵F是等腰直角三角形△ABC斜边BC的中点,
∴AF⊥BC.
又∵三棱柱ABC﹣A1B1C1为直三棱柱,
∴面ABC⊥面BB1C1C,
∴AF⊥面BB1C1C,AF⊥B1F.
设AB=AA1=1,则 ![]() ,EF=
,EF= ![]() ,
, ![]() .
.
∴ ![]() =
= ![]() ,∴B1F⊥EF.
,∴B1F⊥EF.
又AF∩EF=F,∴B1F⊥平面AEF.
而B1F面AB1F,故:平面AB1F⊥平面AEF
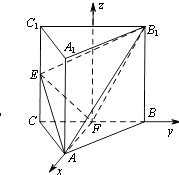
(2)解:以F为坐标原点,FA,FB分别为x,y轴建立直角坐标系如图,
设AB=AA1=1,
则F(0,0,0),A( ![]() ),B1(0,﹣
),B1(0,﹣ ![]() ,1),E(0,﹣
,1),E(0,﹣ ![]() ,
, ![]() ),
),
![]() ,
, ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,1).
,1).
由(1)知,B1F⊥平面AEF,取平面AEF的法向量:
![]() =(0,
=(0, ![]() ,1).
,1).
设平面B1AE的法向量为 ![]() ,
,
由 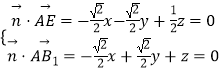 ,
,
取x=3,得 ![]() .
.
设二面角B1﹣AE﹣F的大小为θ,
则cosθ=|cos< ![]() >|=|
>|=| 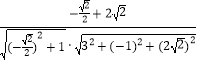 |=
|= ![]() .
.
由图可知θ为锐角,
∴所求二面角B1﹣AE﹣F的余弦值为 ![]() .
.
【解析】(1)连结AF,由已知条件推导出面ABC⊥面BB1C1C,从而AF⊥B1F,由勾股定理得B1F⊥EF.由此能证明平面AB1F⊥平面AEF.(2)以F为坐标原点,FA,FB分别为x,y轴建立直角坐标系,利用向量法能求出二面角B1﹣AE﹣F的余弦值.
【考点精析】掌握平面与平面垂直的判定是解答本题的根本,需要知道一个平面过另一个平面的垂线,则这两个平面垂直.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
【题目】某校举行“庆元旦”教工羽毛球单循环比赛(任意两个参赛队只比赛一场),共有高一、高二、高三三个队参赛,高一胜高二的概率为 ![]() ,高一胜高三的概率为
,高一胜高三的概率为 ![]() ,高二胜高三的概率为P,每场胜负独立,胜者记1分,负者记0分,规定:积分相同者高年级获胜.
,高二胜高三的概率为P,每场胜负独立,胜者记1分,负者记0分,规定:积分相同者高年级获胜.
(Ⅰ)若高三获得冠军概率为 ![]() ,求P.
,求P.
(Ⅱ)记高三的得分为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2﹣ax,g(x)=lnx,h(x)=f(x)+g(x).
(1)若h(x)的单调减区间是( ![]() ,1),求实数a的值;
,1),求实数a的值;
(2)若f(x)≥g(x)对于定义域内的任意x恒成立,求实数a的取值范围;
(3)设h(x)有两个极值点x1 , x2 , 且x1∈(0, ![]() ).若h(x1)﹣h(x2)>m恒成立,求m的最大值.
).若h(x1)﹣h(x2)>m恒成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,直线l的参数方程为 ![]() ,若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos2θ+4cosθ=ρ(ρ≥0,0≤θ≤2π).
,若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos2θ+4cosθ=ρ(ρ≥0,0≤θ≤2π).
(Ⅰ)当 ![]() 时,求直线l的普通方程;
时,求直线l的普通方程;
(Ⅱ)若直线l与曲线C相交A,B两点.求证: ![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|+|2x+5|,且f(x)≥m恒成立.
(Ⅰ)求m的取值范围;
(Ⅱ)当m取最大值时,解关于x的不等式:|x﹣3|﹣2x≤2m﹣8.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cosx,sinx),
=(2cosx,sinx), ![]() =(cosx,2
=(cosx,2 ![]() cosx),函数f(x)=
cosx),函数f(x)= ![]()
![]() ﹣1.
﹣1.
(Ⅰ)求函数f(x)的单调递减区间;
(Ⅱ)在锐角△ABC中,内角A、B、C的对边分别为a,b,c,tanB= ![]() ,对任意满足条件的A,求f(A)的取值范围.
,对任意满足条件的A,求f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°.
(Ⅰ)证明:AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com