Question

【题目】已知﹣ ＜x＜0，则sinx+cosx= ．
（I）求sinx﹣cosx的值；
（Ⅱ）求 的值．

Answer 1

【答案】解：（Ⅰ）由sinx+cosx= ，平方得sin2x+2sinxcosx+cos2x= ，

即2sinxcosx=﹣ ．

∵（sinx﹣cosx）2=1﹣2sinxcosx= ．

又∵﹣ ＜x＜0，∴sinx＜0，cosx＞0，sinx﹣cosx＜0，

故sinx﹣cosx=﹣ ．

（Ⅱ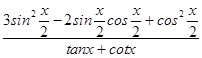） = =sinxcosx（2﹣cosx﹣sinx）

=（﹣ ）×（2﹣ ）=﹣

【解析】（Ⅰ）把sinx+cosx= 两边平方求得sinxcosx的值，进而根据∵（sinx﹣cosx）2=1﹣2sinxcosx求得（sinx﹣cosx）2=，进而根据﹣ ＜x＜0确定sinx﹣cosx的正负，求得答案．（Ⅱ）先把原式中的正切转换成弦，进而根据倍角公式化简整理，把（1）中求得的sinxcosx和sinx﹣cosx代入即可得到答案．
【考点精析】本题主要考查了同角三角函数基本关系的运用的相关知识点，需要掌握同角三角函数的基本关系：；;（3） 倒数关系：才能正确解答此题．