
| A. | ①② | B. | ②④ | C. | ③④ | D. | ①③ |
分析 根据有界泛函数的定义,逐个验证,对于①取x=0,即可说明①不是有界泛函数;对于②采取反证法,f(x)=x2是有界泛函数,则x2≤M|x|,取x=M+1,得到矛盾,因此②不是有界泛函数;对于③利用三角函数的有界性即可证明③是有界泛函数;对于④求函数f(x)=$\frac{x}{{x}^{2}+x+1}$的最大值即可证明④是有界泛函数;从而得到选项.
解答 解:函数f(x)对任意的实数x,存在常数M,使得不等式|f(x)|≤M|x|恒成立,那么就称函数f(x)为有界泛函数,
∴①取x=0,则|f(x)|=1,|x|=0,故不存在常数M,使得不等式|f(x)|≤M|x|成立,因此①不是有界泛函数;
②若f(x)=x2是有界泛函数,则x2≤M|x|,取x=M+1,则有(M+1)2>M(M+1),故与假设矛盾,因此②不是有界泛函数;
③f(x)=(sinx+cosx)x≤$\sqrt{2}$|x|,故③是有界泛函数;
④f(x)=$\frac{x}{{x}^{2}+x+1}$≤$\frac{4}{3}$|x|,故④是有界泛函数;
故选C.
点评 此题是个中档题.考查函数恒成立问题,以及三角函数的有界性和二次函数配方法求最值等基础知识,同时考查了学生的阅读能力,对题意的理解和转化能力,以及灵活应用知识分析解决问题的能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
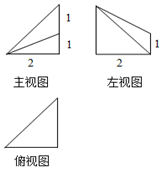
| A. | 2 | B. | $2\sqrt{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点.
如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 30° | C. | 60°或120° | D. | 30°或150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com