
分析 设长方体的长、宽、高分别为a,b,c,由长方体的三个面的面积分别是$\sqrt{2}、\sqrt{3}、\sqrt{6}$,列出方程组求出a,b,c,由此能求出长方体的体积和对角线长.
解答 解:设长方体的长、宽、高分别为a,b,c,
∵长方体的三个面的面积分别是$\sqrt{2}、\sqrt{3}、\sqrt{6}$,
∴$\left\{\begin{array}{l}{ab=\sqrt{6}}\\{ac=\sqrt{3}}\\{bc=\sqrt{2}}\end{array}\right.$,解得a=$\sqrt{3}$,b=$\sqrt{2}$.c=1.
∴长方体的体积V=abc=$\sqrt{3}×\sqrt{2}×1$=$\sqrt{6}$,
对角线长为:$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$=$\sqrt{3+2+1}$=$\sqrt{6}$.
故答案为:$\sqrt{6}$; $\sqrt{6}$.
点评 本题考查长方体的体积、对角线长的求法,是中档题,解题时要认真审题,注意长方体的结构特征的合理运用.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
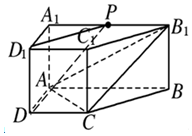 直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.P为A1B1的中点
直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.P为A1B1的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
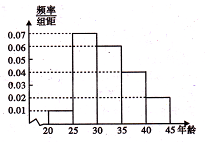 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示:
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com