
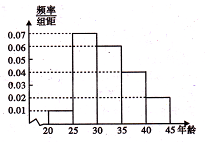
 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示:
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示:分析 (1)由题设利用频率分布直方图能求出第一步组的频率,第4组的频率,第5组的频率.
(2)第3组的人数为300,第4组的人数为200,第5组的人数为100,第3,4,5组共有600名志愿者,利用分层抽样在600名志愿者中抽取6名志愿者,能求出第3,4,5组分别抽取的人数.
(3)设第3组的3位志愿者为A1,A2,A3,第4组的2位志愿者为B1,B2,第5组的1 位志愿者为C1,从六位志愿者中抽两位志愿者,利用列举法能求出第4组至少有一名志愿者被抽中的概率.
解答 解:(1)由题设知第一步组的频率为:0.06×5=0.3,
第4组的频率为0.04×5=0.2,
第5组的频率为0.02×5=0.1.
(2)第3组的人数为0.3×1000=300,
第4组的人数为0.2×1000=200,
第5组的人数为0.1×1000=100,
第3,4,5组共有600名志愿者,
∴利用分层抽样在600名志愿者中抽取6名志愿者,每组抽取的人数分别为:
第3组:$\frac{6}{600}×300=3$,
第4组:$\frac{6}{600}×200=2$,
第5组:$\frac{6}{600}×100=1$,
∴第3,4,5组分别抽取3人,2人,1人.
(3)设第3组的3位志愿者为A1,A2,A3,第4组的2位志愿者为B1,B2,
第5组的1 位志愿者为C1,
则从六位志愿者中抽两位志愿者有:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),
(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,C1),(B1,B2),
(B1,C1),(B2,C1),共15种,
第4组至少有一名志愿者被抽中包含9种情况,
∴第4组至少有一名志愿者被抽中的概率p=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,难度不大,属于基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=|cotx|sinx | B. | $y=cos({2x-\frac{π}{2}})$ | C. | y=sin2x+cos2x | D. | y=tanx-cotx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得顶端O的仰角和立柱底部B的俯角均为30°,已知摄影爱好者的身高约为$\sqrt{3}$米(将眼睛S距地面的距离SA按$\sqrt{3}$米处理)
如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得顶端O的仰角和立柱底部B的俯角均为30°,已知摄影爱好者的身高约为$\sqrt{3}$米(将眼睛S距地面的距离SA按$\sqrt{3}$米处理)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com