
分析 (1)求出直线PQ的斜率,从而求出直线方程即可;(2)通过讨论直线过(0,0)和直线不过(0,0)求出直线方程即可.
解答 解:(1)$P({-2,\sqrt{3}})$,Q(-1,0),
故KPQ=$\frac{\sqrt{3}}{-2-(-1)}$=-$\sqrt{3}$,
故直线PQ的方程是:y=-$\sqrt{3}$(x+1),
即$\sqrt{3}$x+y+$\sqrt{3}$=0;
(2)由直线在x轴,y轴上的截距相等,
则直线不过(0,0)时,
设直线方程是:x+y=a,
将P(2,3)代入方程得:a=5,
故直线方程是:x+y-5=0;
直线过(0,0)时,直线的斜率k=$\frac{3}{2}$,
故直线方程是:y=$\frac{3}{2}$x,即3x-2y=0.
点评 本题考查了求直线方程问题,考查直线的斜率和直线的点斜式方程以及一般式方程,是一道基础题.


科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{9}{19},2}]$ | B. | [-1,2] | C. | $[{-\frac{1}{4},2}]$ | D. | $[{-\frac{1}{4},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-6)2+(y-5)2=10 | B. | (x+6)2+(y+5)2=10 | C. | (x-5)2+(y-6)2=$\sqrt{10}$ | D. | (x+5)2+(y+6)2=$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
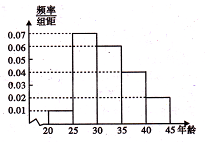 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示:
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com