
| A. | $[{\frac{9}{19},2}]$ | B. | [-1,2] | C. | $[{-\frac{1}{4},2}]$ | D. | $[{-\frac{1}{4},+∞})$ |
分析 利用换元法,转化为二次函数,利用配方法,根据函数的定义域,即可求得函数f(x)的值域.
解答 解:令3x=t,则y=t2-3t+2=(t-$\frac{3}{2}$)2-$\frac{1}{4}$.
∵-1≤x≤1,∴$\frac{1}{3}$≤t≤3.
∴当t=3,即x=1时,y取得最大值2;
当t=$\frac{3}{2}$,即x=$lo{g}_{3}\frac{3}{2}$时,y取得最小值-$\frac{1}{4}$,
∴函数f(x)的值域为[-$\frac{1}{4}$,2].
故选C.
点评 本题考查函数值域的求解,考查换元法的运用,解题的关键是换元转化为二次函数求值域问题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:解答题
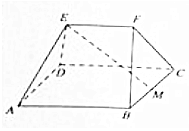 如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.
如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | c>b>a | C. | c>a>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com