
 如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得顶端O的仰角和立柱底部B的俯角均为30°,已知摄影爱好者的身高约为$\sqrt{3}$米(将眼睛S距地面的距离SA按$\sqrt{3}$米处理)
如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得顶端O的仰角和立柱底部B的俯角均为30°,已知摄影爱好者的身高约为$\sqrt{3}$米(将眼睛S距地面的距离SA按$\sqrt{3}$米处理)分析 (1)摄影者眼部记为点S,作SC⊥OB于C,则有∠CSB=30°,∠ASB=60°.SA=$\sqrt{3}$,在Rt△SAB中,由三角函数的定义可求AB;再由SC=3,∠CSO=30°,在Rt△SCO中由三角函数的定义可求OC,进而可求OB
(2由题意可得cos∠MOS=-cos∠NOS,结合余弦定理可得 $\frac{M{O}^{2}+S{O}^{2}-S{M}^{2}}{2MO•SO}$=-$\frac{N{O}^{2}+S{O}^{2}-S{N}^{2}}{2NO•SO}$,于是得SM2+SN2=26,可求∠MSN的最大值.
解答 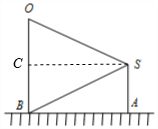 解:(1)如图,不妨将摄影者眼部记为点S,作SC⊥OB于C,
解:(1)如图,不妨将摄影者眼部记为点S,作SC⊥OB于C,
依题意∠CSB=30°,∠ASB=60°.
又SA=$\sqrt{3}$,故在Rt△SAB中,求得BA=3,
即摄影者到立柱的水平距离为3米.…(3分)
由SC=3,∠CSO=30°,在Rt△SCO中,OC=SCtan30°=$\sqrt{3}$,
又BC=SA=$\sqrt{3}$,故OB=2$\sqrt{3}$,即立柱的高度为2$\sqrt{3}$米.…(6分)
(2)∵cos∠MOS=-cos∠NOS
∴$\frac{M{O}^{2}+S{O}^{2}-S{M}^{2}}{2MO•SO}$=-$\frac{N{O}^{2}+S{O}^{2}-S{N}^{2}}{2NO•SO}$,于是得SM2+SN2=26
从而cos∠MSN=$\frac{S{M}^{2}+S{N}^{2}-M{N}^{2}}{2SM•SN}$≥$\frac{S{M}^{2}+S{N}^{2}-M{N}^{2}}{S{M}^{2}+S{N}^{2}}$=$\frac{11}{13}$,
∵∠MSN为锐角,∴∠MSN最大值为arccos$\frac{11}{13}$,
点评 本题考查的是解三角形的应用,解题的关键是准确理解基本概念:仰角俯角问题,熟知锐角三角函数的定义及正弦、余弦定理.


科目:高中数学 来源: 题型:解答题
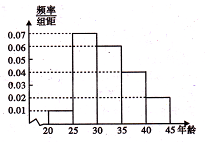 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示:
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=kπ+{(-1)}^{k}•\frac{π}{6}$,k∈Z | B. | $x=2kπ{({-1})^k}•\frac{π}{6}$,k∈Z* | ||
| C. | $x=kπ+{({-1})^{k+1}}•\frac{π}{6}$,k∈Z | D. | $x=2kπ+{({-1})^{k+1}}•\frac{π}{6}$,k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com